题目一:Merge Intervals
题目描述
Given a collection of intervals, merge all overlapping intervals.
Example 1:
Input: [[1,3],[2,6],[8,10],[15,18]] Output: [[1,6],[8,10],[15,18]] Explanation: Since intervals [1,3] and [2,6] overlaps, merge them into [1,6].Example 2:
Input: [[1,4],[4,5]] Output: [[1,5]] Explanation: Intervals [1,4] and [4,5] are considered overlapping.NOTE: input types have been changed on April 15, 2019. Please reset to default code definition to get new method signature.
题目给出一个包含区间的一个列表,其中的区间可能会重合,,要求我们合并这些重合的区间。
我的解法
刚开始理解的重合是部分重合,所以很快就写出来了。后面提交几次才发现还有包含的重合,以及区间的乱序。因此我先将区间按升序排序。然后依次处理不重合、部分重合以及包含重合的情况。
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
if (intervals.size() < 2) return intervals;
vector<vector<int>> ret;
sort(intervals.begin(), intervals.end());
vector<int> temp = intervals[0];
for (int i = 1; i < intervals.size(); i++) {
if (temp[1] < intervals[i][0]) { //不重合
ret.push_back(temp);
temp = intervals[i];
} else if (temp[1] < intervals[i][1]) { //部分重合
temp[1] = intervals[i][1];
} //else 包含重合
}
ret.push_back(temp);
return ret;
}
};
他人解法
官方的sulution有两种,一种是蛮力遍历,并将重合的连接起来,最终合并这些重合的区间。该方法实现复杂且时间复杂度和空间复杂度都较高。因此官方有第二种解法:排序。
没错,就是上面我的解法。时间复杂度为O(nlogn),也就是排序的复杂度。
解法一:sort
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
if (intervals.size() < 2) return intervals;
vector<vector<int>> ret;
sort(intervals.begin(), intervals.end());
ret.push_back(intervals[0]);
for (int i = 1; i < intervals.size(); i++) {
if (ret.back()[1] < intervals[i][0]) {
ret.push_back(intervals[i]);
} else {
ret.back()[1] = max(ret.back()[1], intervals[i][1]);
}
}
return ret;
}
};
题目二:Insert Interval
题目描述
Given a set of non-overlapping intervals, insert a new interval into the intervals (merge if necessary).
You may assume that the intervals were initially sorted according to their start times.
Example 1:
Input: intervals = [[1,3],[6,9]], newInterval = [2,5] Output: [[1,5],[6,9]]Example 2:
Input: intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8] Output: [[1,2],[3,10],[12,16]] Explanation: Because the new interval [4,8] overlaps with [3,5],[6,7],[8,10].NOTE: input types have been changed on April 15, 2019. Please reset to default code definition to get new method signature.
题目接着上一题,给出一个包含多个区间的列表和一个区间,其中列表中的区间都不重合,且都是按照区间下限升序排序的,现在要求我们将新给出的区间插入列表,要求保持列表中区间不重合(可能会发生合并)
我的解法
这道题目的难度是hard,但是我觉得不是很难,我很快就用多重if-else写出了程序,虽然没有调通。但是我的思路是正确的。只是我写得太复杂了,自己都很难理清。当我看了一遍讨论区后才恍然大悟,原来可以这样。
他人解法
解法一
- 使用新区间的第1个数与列表中区间的第2个数比较,找到头重合的区间
- 使用新区间的第2个数与列表中区间的第1个数比较,找到尾重合的区间
- 头重合的区间之前以及尾重合的区间之后的区间都逐个复制
- 实时更新新区间的第2个数(第1个数只要更新1次)
class Solution {
public:
vector<vector<int>> insert(vector<vector<int>>& intervals, vector<int>& newInterval) {
vector<vector<int>> ret;
int s = 0;
while (s < intervals.size() && newInterval[0] > intervals[s][1]) {
ret.push_back(intervals[s++]); //前面不重合
}
if (s < intervals.size()) { //遇到头重合的区间
newInterval[0] = min(newInterval[0], intervals[s][0]);
}
//寻找尾重合的区间
while (s < intervals.size() && newInterval[1] >= intervals[s][0]) {
newInterval[1] = max(newInterval[1], intervals[s][1]);
s++;
}
ret.push_back(newInterval);
while (s < intervals.size()) {
ret.push_back(intervals[s++]);
}
return ret;
}
};
解法二:直接更改原列表
不适用额外的空间,直接再参数给出的列表中操作。看似更简单明了,实则不然。因为给出的是列表或者说是数组,其在内存中的空间是连续的,而我们向其中插入或删除一个值都要将后面一长串的元素都移动位置。所以该算法的时间复杂度应该为O(n^2)
public List<Interval> insert(List<Interval> intervals, Interval newInterval) {``
int i=0;
while(i<intervals.size() && intervals.get(i).end<newInterval.start) i++;
while(i<intervals.size() && intervals.get(i).start<=newInterval.end){
newInterval = new Interval(Math.min(intervals.get(i).start, newInterval.start), Math.max(intervals.get(i).end, newInterval.end));
intervals.remove(i);
}
intervals.add(i,newInterval);
return intervals;
}
解法三:equal_range
该算法也是在原有的列表中直接操作,但是其复杂度不是O(n^2),而是O(n)。
该函数原型equal_range (ForwardIterator first, ForwardIterator last, const T& val, Compare comp);
其中first、last是已经排好序的迭代器的第一个和最后一个元素,val是用于比较的元素,而comp就是比较的规则(可以自定义,二元函数. 接受两个参数,返回bool. 表明是否第一个参数应该排在第二个参数的前面.此函数不能修改任何参数的内容.这个参数可以是一个函数指针或者函数对象.)。
当我们定义好比较的规则,执行该函数会得到一个区间。在该区间插入不会影响原列表的有序性。
它返回一对迭代器i和j,其中i是在不破坏次序的前提下,value可插入的第一个位置(亦即lower_bound),j则是在不破坏次序的前提下,value可插入的最后一个位置(亦即upper_bound),因此,[i,j)内的每个元素都等同于value,而且[i,j)是[first,last)之中符合此一性质的最大子区间
class Solution {
public:
vector<vector<int>> insert(vector<vector<int>>& intervals, vector<int>& newInterval) {
if(intervals.size()==0) return {newInterval};
auto compare = [] (const vector<int>&intv1, const vector<int>&intv2)
{ return intv1[1] < intv2[0]; };
auto range = equal_range(intervals.begin(), intervals.end(), newInterval, compare);
auto itr1 = range.first, itr2 = range.second;
if (itr1 == itr2) {
intervals.insert(itr1, newInterval);
} else {
itr2--;
*(itr2->begin()+0) = min(newInterval[0], *(itr1->begin()+0));
*(itr2->begin()+1) = max(newInterval[1], *(itr2->begin()+1));
intervals.erase(itr1, itr2);
}
return intervals;
}
};
题目三:Sort Colors
题目描述
Given an array with n objects colored red, white or blue, sort them in-place so that objects of the same color are adjacent, with the colors in the order red, white and blue.
Here, we will use the integers 0, 1, and 2 to represent the color red, white, and blue respectively.
Note: You are not suppose to use the library’s sort function for this problem.
Example:
Input: [2,0,2,1,1,0] Output: [0,0,1,1,2,2]Follow up:
- A rather straight forward solution is a two-pass algorithm using counting sort. First, iterate the array counting number of 0’s, 1’s, and 2’s, then overwrite array with total number of 0’s, then 1’s and followed by 2’s.
- Could you come up with a one-pass algorithm using only constant space?
题目给出一个列表,其中只包含0、1、2 三个值,这三个值是随机排列。现在要求我们将其排序。但是单纯地排序可能太简单了,所以题目要求我们仅使用额定空间遍历一遍就将其排序。
我的解法
直接排序很容易,随便试了一下冒泡排序,以及自创冒泡排序都能通过,可是时间复杂度为$O(n^2)$, 这不是题目原本的意思。
他人解法
解法一
由于只有三个数(0、1、2),因此我们可以只管0和2。0一定是在最前面,2一定是在最后面。我们从左到右依次扫描,遇到0就将其交换到前面,遇到2就交换到后面。
class Solution {
public:
void sortColors(vector<int>& nums) {
int zero = 0, second = nums.size() - 1;
for (int i = 0; i <= second; i++) {
while (2 == nums[i] && i < second) {
swap(nums[i], nums[second--]);
}
while (0 == nums[i] && i > zero) {
swap(nums[i], nums[zero++]);
}
}
}
};
解法二
解法二也是基于解法一的思路,不过是更易于理解,不像解法一那么有点抽象。
class Solution {
public:
void sortColors(vector<int>& nums) {
if (nums.size() < 2) return;
int zero = 0, two = nums.size() - 1;
for (int i = 0; i <= two;) {
if (nums[i] == 0) {
if (nums[zero] != 0) {
swap(nums[zero], nums[i]);
}
zero++;i++;
} else if (nums[i] == 2) {
if (nums[two] != 2) {
swap(nums[two], nums[i]);
}
two--;
} else {
i++;
}
}
}
};
题目四:Insertion Sort List
题目描述
Sort a linked list using insertion sort.
A graphical example of insertion sort. The partial sorted list (black) initially contains only the first element in the list. With each iteration one element (red) is removed from the input data and inserted in-place into the sorted list
Algorithm of Insertion Sort:
- Insertion sort iterates, consuming one input element each repetition, and growing a sorted output list.
- At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list, and inserts it there.
- It repeats until no input elements remain.
Example 1:
Input: 4->2->1->3 Output: 1->2->3->4Example 2:
Input: -1->5->3->4->0 Output: -1->0->3->4->5
题目给出一个链表,要求我们使用插入排序使之呈升序状态。
我的解法
目前来看我对链表的运用还是火候不够啊,一个简单的插入排序我都要搞那么久。
链表不同于数组,其在内存中不是连续存储,而是使用指针将各个结点按顺序连接起来。我们更改链表的顺序本质上就是更改相关结点的next指针。
我们首先回忆一下插入排序算法:插入排序将初始数据分为已排序数据和待排序数据两大部分,初始状态已排序数据为空,待排序数据为整个初始数据。然后我们按照一定顺序从待排序数据中取数据插入到已排序数据中,因此已排序数据+1,待排序数据-1。重复这个过程直到待排序数据为空,此时初始数据已经全部有序。
我们要更改一个结点在链表中的位置,需要更改3个指针:
- 该结点的next指针
- 原本指向该结点的next指针
- 待插入位置之前结点的next指针
比如:
1 -> 3 -> 4 -> 5 -> 二 -> 6 要将2排序
1 -> 二 -> 3 -> 4 -> 5 -> 6
首先一定是将结点5的next指针由2改成6 1 -> 3 -> 4 -> 5 -> 6 <- 2
然后将结点2的next指针由6改成3(之前找到的) 1 -> 3 -> 4 -> 5 -> 6
^
2
最后将结点1的next指针由3改成2 1 -> 2 -> 3 -> 4 -> 5 -> 6
因此我们必须定义变量提前保存1、5这两个结点的值。这里我将其分别定义为spre和cpre
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* insertionSortList(ListNode* head) {
if (!head || !head->next) return head;
ListNode *cur = head->next, *cpre = head;
while (cur) {
ListNode *sorted = head, *spre = nullptr, *cnext = cur->next;
while (sorted != cnext) {
if (cur->val < sorted->val) {
cpre->next = cur->next;
cur->next = sorted;
if (spre) {
spre->next = cur;
} else {
head = cur;
}
break;
}
sorted = sorted->next;
spre = spre ? spre->next : head;
}
if (cur->val >= cpre->val) {
cpre = cur;
}
cur = cnext;
}
return head;
}
};
他人解法
解法一
本质上和我的解法相同,唯一高明一点的地方是使用NULL将已排序的部分与待排序的部分分开,使得代码看起来比较容易理解。其实该算法的curNext也能起到和NULL一样的效果。
另外,我上面的解法是统一处理插在已排序n个结点前面位置的情况(n个已排序结点有n-1个位置可插入),最后处理插在已排序的最后结点后面位置的特殊情况;而该算法是优先处理插在已排序结点第1个结点前面的特殊情况,然后才统一处理排在这些已排序结点后面的情况。
class Solution {
public:
ListNode *insertionSortList(ListNode *head) {
if (head == NULL || head->next == NULL)
return head;
ListNode *cur = head->next;
head->next = NULL; // split the sorted and unsorted
while (cur != NULL) {
ListNode *curNext = cur->next; //store the next node to be inserted
ListNode *sorted = head;
if (cur->val < sorted->val) { //node cur should be the new head
cur->next = sorted;
head = cur;
}
else {
while (sorted->next && sorted->next->val <= cur->val)
sorted = sorted->next;
cur->next = sorted->next;
sorted->next = cur;
}
cur = curNext;
}
return head;
}
};
解法二:递归
什么时候都不要忘记递归,真的!
上面我们已经分析出了待排序结点要插入到已排序结点中只有两种情况,一种是统一插入到结点后面(前面),另一种就是直接插入作为新的头结点(尾结点),所以我们递归实现的思路也有了,就是处理这两种情况。
不过递归有的时候真的很难想到思路。
class Solution {
public:
ListNode* insertionSortList(ListNode* head) {
if (nullptr == head || nullptr == head->next) return head;
ListNode* h = insertionSortList(head->next);
if (head->val <= h->val) { //case 1: new head
head->next = h;
return head;
} else { // case 2: others
ListNode *node = h;
while (node->next && node->next->val < head->val) {
node = node->next;
}
head->next = node->next;
node->next = head;
return h;
}
}
};
题目五:Sort List
题目描述
Sort a linked list in O(n log n) time using constant space complexity.
Example 1:
Input: 4->2->1->3 Output: 1->2->3->4Example 2:
Input: -1->5->3->4->0 Output: -1->0->3->4->5
题目描述很简单,就是给出一个链表要我们排序。但是有两个条件不简单:
- 时间复杂度为
O(nlogn) - 空间复杂度为
O(1)
我的解法
i have no ideaaa!不过依我看来,假如我以上面的插入排序为基准(时间复杂度为O(n^2)),要想达到这两个条件,只有一个可能,那就是利用已排序序列已经排好序的性质,在寻找待插入结点的过程中使用二分查找。不过这是链表而不是数组,二分查找完全不能用啊!怎么办?
他人解法
解法一:自底向上的分治法
我们知道只包含一个结点的链表肯定是有序的,所以我们就基于1个结点开始,将第1、2个结点作为一组使其有序;将第3、4个结点作为一组使其有序;若最后剩余一个结点就本身有序。这样两两有序后,再将原来的两组合并起来变成一个大组并保持有序。依次循环直到最后只剩两组(可能第二组元素个数不足,但是有序),继续其合并就得到我们想要的结果了。
要得到上面的小组我们需要定义类似于split之类的函数,split(cur, step)表示将包括cur在内的step个结点与其后面的结点分离,并返回分离后后面链表的头结点。
而要使得链表有序,我们还要定义类似merge之类的函数,merge(l1, l2, head)表示将l1、l2两条有序链表合并成一条有序链表并接在head之后。并返回得到的链表的尾结点。
class Solution {
ListNode* split(ListNode* cur, int step) {
for(int i = 1; cur && i < step; i++) {
cur = cur->next;
}
if (nullptr == cur) return nullptr;
ListNode *second = cur->next;
cur->next = nullptr;
return second;
}
ListNode* merge(ListNode* l1, ListNode* l2, ListNode* head) {
ListNode *cur = head;
while (l1 && l2) {
if (l1->val <= l2->val) {
cur->next = l1;
l1 = l1->next;
} else {
cur->next = l2;
l2 = l2->next;
}
cur = cur->next;
}
cur->next = l1 ? l1 : l2;
while (cur->next) {
cur = cur->next;
}
return cur;
}
public:
ListNode* insertionSortList(ListNode* head) {
if (nullptr == head || nullptr == head->next) return head;
int len = 0;
ListNode *cur = head;
ListNode dummy(0);
dummy.next = head;
ListNode *left, *right, *tail;
//the length of the linked-list
while (cur) {
len++;
cur = cur->next;
}
for (int step = 1; step < len; step = step<<1) {
cur = dummy.next;
tail = &dummy;
while (cur) {
left = cur;
right = split(cur, step);
cur = split(right, step);
tail = merge(left, right, tail);
}
}
return dummy.next;
}
};
- 时间复杂度
O(nlogn) - 空间复杂度
O(1)
请问这是中等难度吗?要我在面试的时候二十分钟写出来这玩意儿,抱歉我恐怕做不到呢
解法二、插入排序
Keep a sorted partial list (
head) and start from the second node (head -> next), each time when we see a node withvalsmaller than its previous node, we scan from theheadand find the position that the node should be inserted. Since a node may be inserted beforehead, we create adummyhead that points tohead.
class Solution {
public:
ListNode* sortList(ListNode* head) {
ListNode dummy(0);
dummy.next = head;
ListNode *pre = &dummy, *cur = head;
while (cur) {
if (cur->next && cur->next->val < cur->val) {
while (pre->next && pre->next->val < cur->next->val) {
pre = pre->next;
}
ListNode* temp = cur->next;
cur->next = temp->next;
temp->next = pre->next;
pre->next = temp;
pre = &dummy;
} else {
cur = cur->next;
}
}
return dummy.next;
}
};
很遗憾插入排序的时间复杂度为O(n^2),没有完成题目的条件。
题目六:Maximum Gap
题目描述
Given an unsorted array, find the maximum difference between the successive elements in its sorted form.
Return 0 if the array contains less than 2 elements.
Example 1:
Input: [3,6,9,1] Output: 3 Explanation: The sorted form of the array is [1,3,6,9], either (3,6) or (6,9) has the maximum difference 3.Example 2:
Input: [10] Output: 0 Explanation: The array contains less than 2 elements, therefore return 0.Note:
- You may assume all elements in the array are non-negative integers and fit in the 32-bit signed integer range.
- Try to solve it in linear time/space.
题目给出一个未排序的数组,数组中的的元素都是非负整数,要求得到大小相邻的元素的最大差值,如1、5、4、9、0,大小相邻的元素排列是0、1、4、5、9,其中0、1的差值为1,1、4的差值为3,4、5的差值为1,5、9的差值为4,所以该数组的中的元素的最大差值为4。
我的解法
题目要求用线性时间解答,也就是O(n)的时间复杂度。但是这怎么可能呢,单是一个排序就要我O(nlgn)的时间了,除非他不用排序。但是以我现在的能力,我只能想出先使用排序的手段,然后再从左到右依次遍历元素,从而得到最大差值。
class Solution {
public:
int maximumGap(vector<int>& nums) {
if (nums.size() < 2) return 0;
sort(nums.begin(), nums.end());
int ret = 0;
for (int i = 1; i < nums.size(); i++) {
ret = max(ret, nums[i]-nums[i-1]);
}
return ret;
}
};
他人解法
其实做到这题的时候,我看到线性空间和时间就傻了,因此我立马放下当前题目找了关于线性排序算法的文章,甚至下载了算法导论来看。很幸运我很快就找到了答案,那就是三种线性时间复杂度排序算法——计数排序、基数排序和桶排序。在看这些算法理论推导的过程中我又发现我对渐进符号的理解好像不太准确,比如$n=O(n^2)$,意思是n的函数在大于一定值后其函数不高于$kn^2$,简单来说就是大O符号等号左边的函数的上界是$n^2$。还有$\Theta、O、\Omega、o、\omega$等等,这些其实表示的都是函数集合,而我们的等号其实本质是$\in$符号,等等。具体内容看我前面一篇文章:算法基础之渐进符号
搞懂了渐进符号就能愉快地看算法推导了(太难的推导跳过)。经过几天的摸索,我搞懂了计数排序基数排序桶排序以及它们的一般应用场景。其中计数排序最为简单,不需要其它算法辅助,缺点是仅限于较小的一个区间内元素的排序。桶排序和基数排序都需要辅以其它排序算法,而基数排序又常常使用计数排序作为辅助。桶排序需要输入的数据足够均匀分布,否则达不到线性的条件。因此我觉得基数排序才是老大。具体分析看这篇文章:线性时间排序算法(计数排序、基数排序、桶排序)
解法一:基数排序+计数排序
我首先试了一下直接使用计数排序,结果是超时,因为给出的case区间太大,而时间限制太小,虽然算法是$O(n)$的,但由于体量和运行时间的限制,这里无法体现。
因此我们采用基数排序,并使用计数排序加以辅助,顺利通过!
class Solution {
public:
int maximumGap(vector<int>& nums) {
int n = nums.size();
if (n < 2) return 0;
int exp = 1, radix = 10;
int maxNum = *max_element(nums.begin(), nums.end());
while (maxNum/exp) {
vector<int> count(radix,0);
for (int num : nums) {
count[(num/exp) % 10]++;
}
for (int i = 1; i < count.size(); i++) {
count[i] += count[i-1];
}
vector<int> temp(n, 0);
for (int i = n-1; i >= 0; i--) {
temp[--count[(nums[i]/exp) % 10]] = nums[i];
}
for (int i = 0; i < nums.size(); i++) {
nums[i] = temp[i];
}
exp *= 10;
}
int maxGap = 0;
for (int i = 1; i < nums.size(); i++) {
maxGap = max(maxGap, nums[i] - nums[i-1]);
}
return maxGap;
}
};
解法二:桶排序
其实这道题使用桶排序来做最为合适不过了,因为桶中甚至不需要排序只要记录最大值和最小值。具体来说,题目要求的是排序状态下相邻元素之间的最大差值。假设待排的元素有$n$个,其中最小值为$min$,最大值为$max$,我们要求的最大差值为$maxGap$,通过简单分析可以得到$maxGap \ge (max-min)/(n-1)$.
这个结论是怎么来的呢?我们仔细想想,这$n$个数在什么情况下的$maxGap$最小呢?不难想到,如果这$n$个数两两不同,并且均匀分布(两两之间的间隔相同),这个时候$n$个数之间有$n-1$个$gap$,每一个$gap$都相同,等于$(max-min)/(n-1)$。当然,这里$max-min$可能会小于$n-1$,那么此时我们只能将桶的大小设为$1$了;否则的话我们就令桶的大小为$(max-min)/(n-1)$,这样我们就不用担心桶内的数据了,此时我们只需要记录桶中的最大值和最小值,最大gap一定是在桶之间,也就是上一个桶的最大值与下一个桶的最小值之差。如果不巧碰到$maxGap$恰好等于$(max-min)/(n-1)$,此时桶的大小确实是等于$maxGap$,但是桶与桶之间也是$maxGap$,因为此时元素是均匀分布的。
class Solution {
public:
class Bucket {
public:
bool used = false;
int minval = numeric_limits<int>::max(); // same as INT_MAX
int maxval = numeric_limits<int>::min(); // same as INT_MIN
};
int maximumGap(vector<int>& nums) {
if (nums.empty() || nums.size() < 2)
return 0;
int mini = *min_element(nums.begin(), nums.end()),
maxi = *max_element(nums.begin(), nums.end());
int bucketSize = max(1, (maxi - mini) / ((int)nums.size() - 1)); // bucket size or capacity
int bucketNum = (maxi - mini) / bucketSize + 1; // number of buckets
vector<Bucket> buckets(bucketNum);
for (auto&& num : nums) {
int bucketIdx = (num - mini) / bucketSize; // locating correct bucket
buckets[bucketIdx].used = true;
buckets[bucketIdx].minval = min(num, buckets[bucketIdx].minval);
buckets[bucketIdx].maxval = max(num, buckets[bucketIdx].maxval);
}
int prevBucketMax = mini, maxGap = 0;
for (auto&& bucket : buckets) {
if (!bucket.used)
continue;
maxGap = max(maxGap, bucket.minval - prevBucketMax);
prevBucketMax = bucket.maxval;
}
return maxGap;
}
};
题目七:Largest Number
题目描述
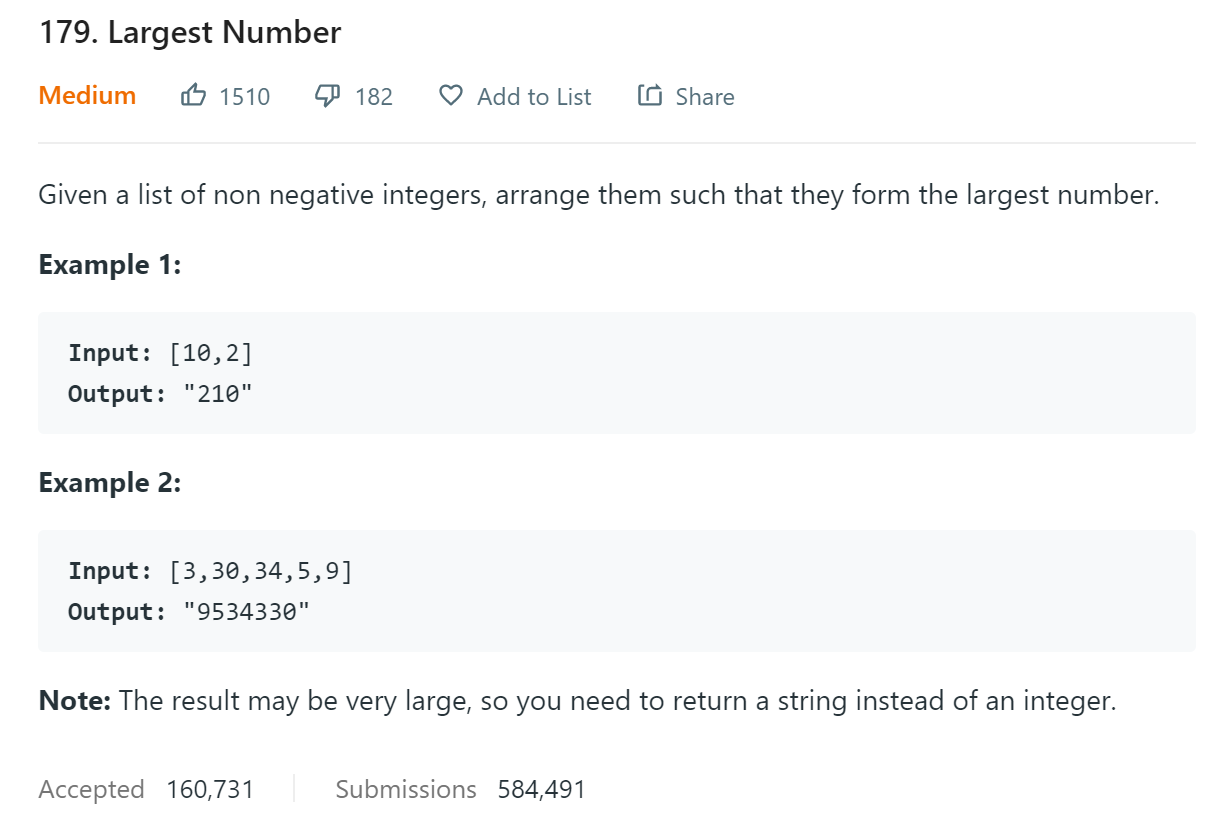
题目给出一个非负整数数组,要求我们使用这些整数拼接成一个最大的数值。由于数值过大,题目说明我们可以以字符串的形式返回。
我的解法
刚开始我就想到首先就将整数转换成字符串,然后利用字符串按从大到小的顺序排序,最后再一个接一个的拼接就好了。但事实不是这样,比如[”121“, ”12“]已经是按字符串逆序排序的,但是很明显”12112“ < “12121”,如果要直接找到排序的规律,真的是很难。
于是不得已我去看了讨论区,一个最高票的java代码,他也是利用字符串排序,不过他是自定义排序规则:
原本的排序规则是s1 > s2,那么s1就排在s2前面,反之就排在后面。
而他的自定义排序规则是这样:
str1 = s1 + s2
str2 = s2 + s2
如果str1 > str2,那么说明s1排在前面所得到的字符串更大,因此将s1排在s2前面
如果str2 < str1,那么说明s2排在前面所得到的字符串更大,因此将s2排在s1前面
利用这一排序规则,我们就可以将所有的字符串按照正确的位置排列起来,最后再依次串联这些字符串得到结果。
class Solution {
vector<string> toString(vector<int> nums) {
vector<string> ret;
for (int num : nums) {
string temp;
if (num == 0) {
ret.push_back("0");
} else {
while (num) {
char c = num%10 + '0';
temp.insert(temp.begin(), c);
num /= 10;
}
ret.push_back(temp);
}
}
return ret;
}
static bool cmp(const string& s1, const string& s2) {
string str1 = s1 + s2;
string str2 = s2 + s1;
return str1 > str2;
}
public:
string largestNumber(vector<int>& nums) {
string ret;
vector<string> strings = toString(nums);
sort(strings.begin(), strings.end(), cmp);
for (string s : strings) {
ret += s;
}
int s = 0;
while (ret[s] == '0' && s < ret.size()) {
s++;
}
if (s < ret.size()) {
return ret.substr(s);
}
return "0";
}
};
他人解法
解法一:一样但是更精简
class Solution {
public:
string largestNumber(vector<int> &num) {
vector<string> arr;
for(auto i:num)
arr.push_back(to_string(i));
sort(begin(arr), end(arr), [](string &s1, string &s2){ return s1+s2>s2+s1; });
string res;
for(auto s:arr)
res+=s;
if(res[0] == '0') return "0";
return res;
}
};
虽然我们的做法几乎一模一样,但是他的却比我的简洁很多。主要原因有两点:
- 我是自定义的整数数组转为字符串数组,而他是调用系统的to_string函数
- 我把比较规则定义为一个静态函数,写在类中;他是直接把规则写在sort函数的第3个参数上
其它解法都是同样的思路,因为这是目前的最优方案。当然还有一些不同的解法,比如遍历,每次遍历完一遍选择一个最大的,然后遍历剩下的选择次大的……
题目八:Valid Anagram
题目描述
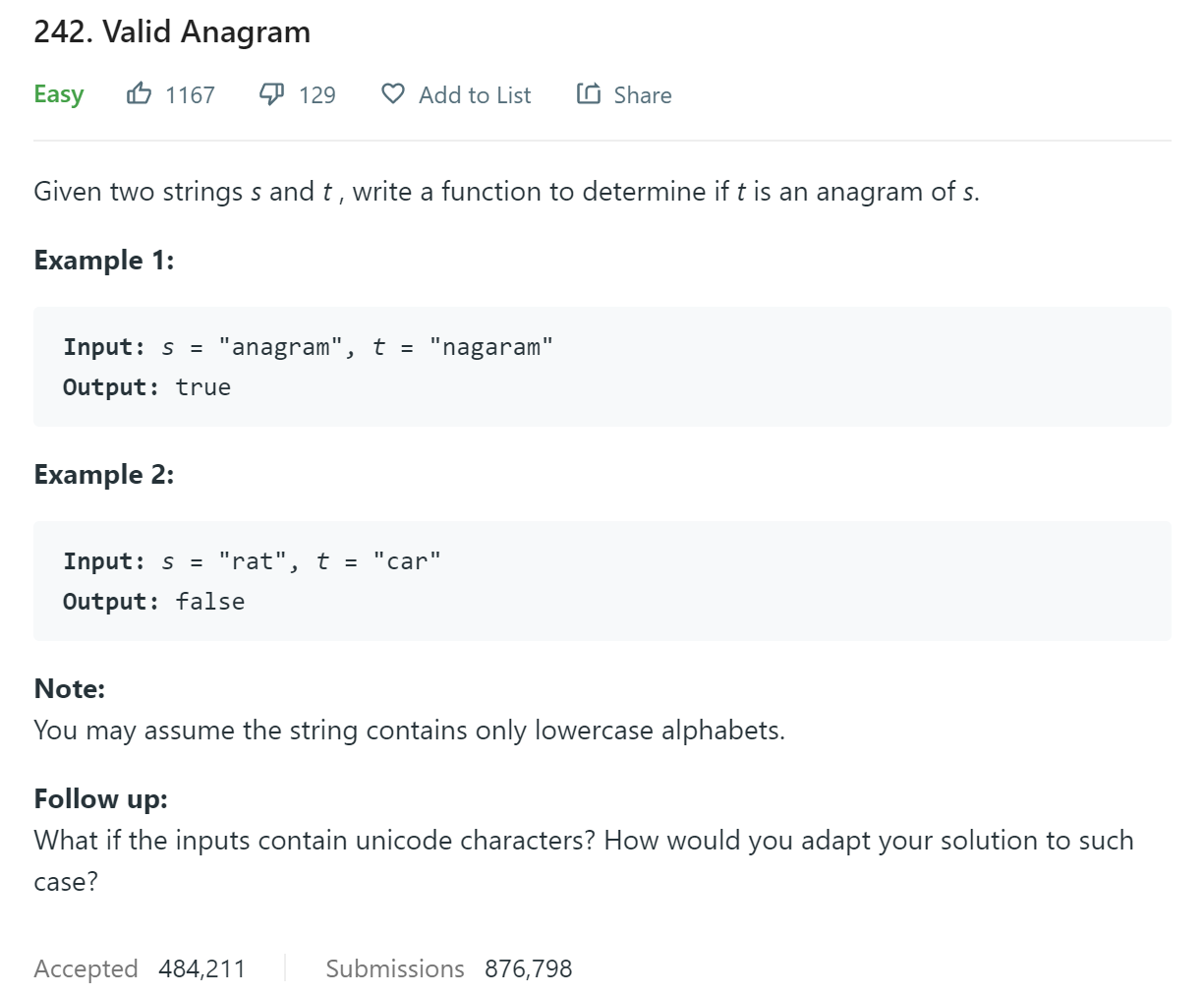
题目中的anagram我不知道什么意思,翻一下是字谜,于是我就迷了。所以我就去看了leetcode中文网站的原题,才知道原来anagram表示的是字母异位词,即比较给出的两个词是不是长度以及组成的字母都一样,只是字母的排列不一样。
我的解法
首先遍历第一个单词,统计出现的每个字母及其次数;然后遍历另一个单词,看看其字母及其次数与第一个单词是否吻合。如果两者组成的字母以及出现次数都相同,那么就返回true,否则返回false
具体实现是把26个英文字母映射到一个大小为26的整型数组chars中,chars[0]表示a出现的次数、chars[25]表示z出现的次数。数组初始化为0,统计完第一个单词后,统计第二个单词的时候,我们使用减一操作而不是加一,这样如果两个单词是字母异位词,那么减一后chars数组最终会回到初始化状态(全部为0)。
class Solution {
public:
bool isAnagram(string s, string t) {
vector<int> chars(26, 0);
for (char c : s) {
chars[c-'a']++;
}
for (char c : t) {
chars[c-'a']--;
}
for (int num : chars) {
if (num != 0) {
return false;
}
}
return true;
}
};
他人解法
解法一:排序
看起来简单明了,但时间复杂度为$O(nlgn)$,n为两个字符串中较长的长度。
class Solution {
public:
bool isAnagram(string s, string t) {
if (s.length() != t.length()) {
return false;
}
sort(s.begin(), s.end());
sort(t.begin(), t.end());
return s == t;
}
};
解法二:哈希表
几乎和我的一模一样啊!但是该算法更聪明的一点是第一步先判断两个单词的长度是否相等,然后是在两个单词长度相等的前提下,在一个for循环里面处理加一和减一操作。非常聪明!
public boolean isAnagram(String s, String t) {
if (s.length() != t.length()) {
return false;
}
int[] counter = new int[26];
for (int i = 0; i < s.length(); i++) {
counter[s.charAt(i) - 'a']++;
counter[t.charAt(i) - 'a']--;
}
for (int count : counter) {
if (count != 0) {
return false;
}
}
return true;
}
解法三:解法二的改进版
在算法二的基础上将两个for循环分开,这样当处理第二个for循环时,由于是减一操作,因此只要出现小于0的情况,后续就不可能复原为0了。因此可以直接返回false。
public boolean isAnagram(String s, String t) {
if (s.length() != t.length()) {
return false;
}
int[] table = new int[26];
for (int i = 0; i < s.length(); i++) {
table[s.charAt(i) - 'a']++;
}
for (int i = 0; i < t.length(); i++) {
table[t.charAt(i) - 'a']--;
if (table[t.charAt(i) - 'a'] < 0) {
return false;
}
}
return true;
}
题目九:Count of Smaller Numbers After Self
题目描述
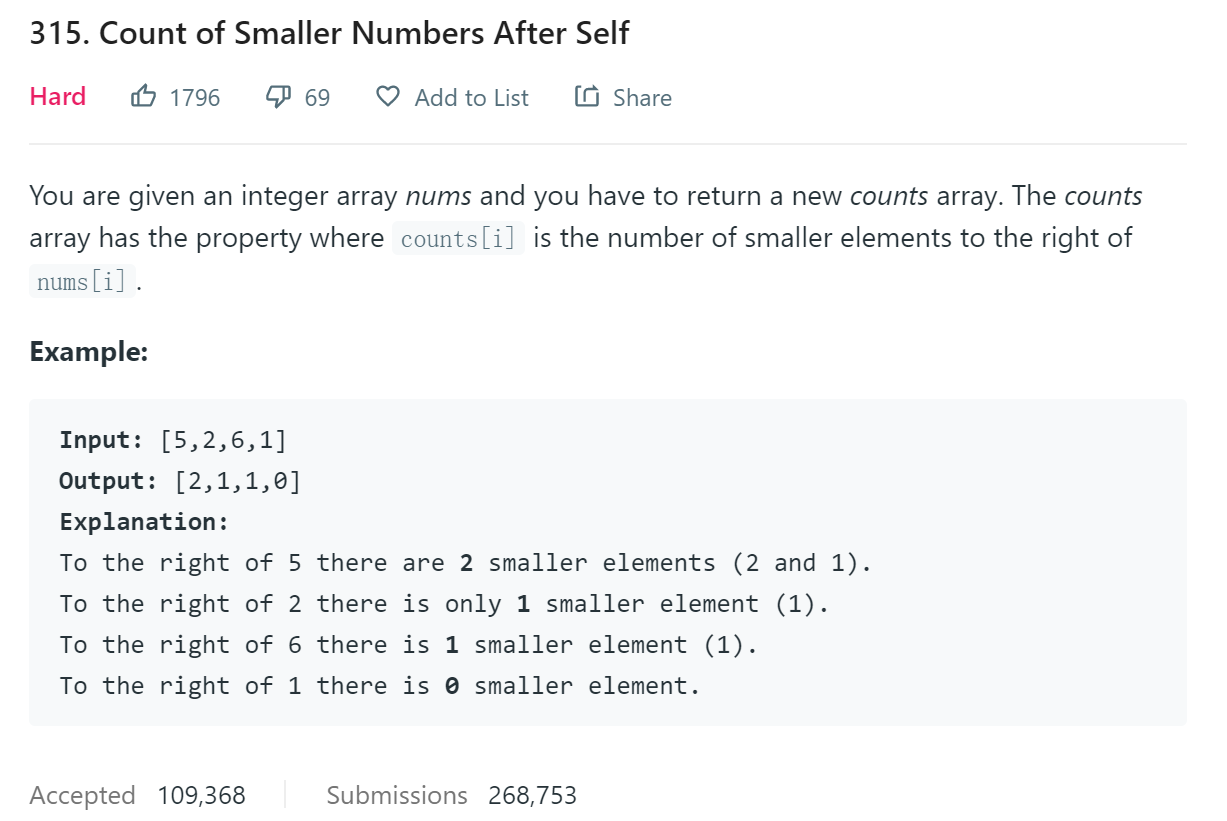
题目给出一个整数数组,要我们求出数组中每一个元素的右边所有元素中小于该元素的数量。看似简单吧?实则巨难啊!!
我的解法
不看评论区根本想不到其它解法,只有准暴力遍历。
class Solution {
public:
vector<int> countSmaller(vector<int>& nums) {
if (nums.size() < 1) return {};
int n = nums.size();
vector<int> ret(n, 0);
for (int i = n-1; i >= 0; i--) {
for (int j = n-1; j > i; j--) {
if (nums[j] < nums[i]) {
ret[i]++;
}
}
}
return ret;
}
};
他人解法
解法一:BST
我们先看最朴素的解法,从后向前遍历数组,每次都在当前元素后面再遍历一遍得到小于该元素的元素个数。因此时间为$O(n^2)$,实现很简单,但是过不去。如果我们把当前元素右边所有元素都维护成一个有序序列,那么我们就可以使用诸如二分查找之类的技巧得到$O(nlgn)$的效果。这个有序序列我们不能使用链表,因为链表不能直接存取,因此不能二分查找;也不能使用数组,因为我们还需要插入元素,数组的元素插入会导致该元素后面整个右移,时间复杂度为$O(n^2)$。什么数据结构能有效地兼顾查找与插入的效率呢?
没错,就是二叉排序树。
BST(二叉排序树)我们之前讲过,这里就不讲具体实现了。但是由于BST中是没有相等的结点值,而该题目中很有可能会出现重复的值,因此我们需要对结点做特殊处理。
我们定义一个结点除了左右两个子节点还有val、sum、dup三个整数,这三个整数分别表示当前结点值、左子树中结点数、与该结点相等的结点数。
虽然是用递归实现的,但是总体思路很简单,就是找到应该插入的位置,然后将一路上的结点及其左子树的结点数加起来就得到小于当前插入结点的结点数。但是我们插入的地方有两个,一个是作为叶结点插入。因此我们需要好好维护BST中每个结点的dup和sum值。
当时我在想为什么不会插入在中间结点,而一定是叶子结点呢?后面我仔细想想,发现同样的一组数可以组成不同结构的BST,原因就在于插入顺序。比如:
插入顺序:1 2 3 1 3 2
1 1
\ \
2 3
\ /
3 2
因此插入的过程是不会出现插入为中间结点的情况的。
class Solution {
public:
class Node {
public:
Node *left, *right;
int val, sum, dup = 1;
Node(int v, int s) {
this->val = v;
this->sum = s;
left = nullptr;
right = nullptr;
}
};
Node* insert(Node* root, vector<int> &ret, int i, int num, int preSum) {
if (root == nullptr) {
ret[i] = preSum;
return new Node(num, 0);
} else if (num == root->val) {
root->dup++;
ret[i] = preSum + root->sum;
} else if (num < root->val) {
root->sum++;
root->left = insert(root->left, ret, i, num, preSum);
} else {
root->right = insert(root->right, ret, i, num, preSum + root->sum + root->dup);
}
return root;
}
vector<int> countSmaller(vector<int>& nums) {
if (nums.empty()) return {};
vector<int> ret(nums.size(), 0);
Node *root = nullptr;
for (int i = nums.size()-1; i >= 0; i--) {
root = insert(root, ret, i, nums[i], 0);
}
return ret;
}
};
迭代版
同样的思路,但是迭代法看起来更加直观。
class Solution {
public:
class Node {
public:
int val, count = 0, leftSum = 0;
Node *left = nullptr, *right = nullptr;
Node(int val) {
this->val = val;
}
};
int insert(Node* root, int num) {
int sum = 0;
while (root->val != num) {
if (num < root->val) {
if (root->left == nullptr) {
root->left = new Node(num);
}
root->leftSum++;
root = root->left;
} else {
sum += root->leftSum + root->count;
if (root->right == nullptr) {
root->right = new Node(num);
}
root = root->right;
}
}
root->count++;
return sum + root->leftSum;
}
vector<int> countSmaller(vector<int>& nums) {
int n = nums.size();
if (n <= 0) return {};
vector<int> ret(n, 0);
Node *bst = new Node(nums[n-1]);
for (int i = n-1; i >= 0; i--) {
ret[i] = insert(bst, nums[i]);
}
return ret;
}
};
解法二:插入排序
这或许是最简单的解法。
class Solution {
public:
vector<int> countSmaller(vector<int>& nums) {
int n = nums.size();
if (n < 1) return {};
vector<int> temp;
vector<int> ret(n, 0);
temp.push_back(nums[n-1]);
for (int i = n-2; i >= 0; i--) {
if (nums[i] <= temp[0]) {
ret[i] = 0;
temp.insert(temp.begin(), nums[i]);
continue;
}
for (int j = temp.size()-1; j >= 0; j--) {
if (temp[j] < nums[i]) {
ret[i] = j + 1;
temp.insert(temp.begin()+j+1, nums[i]);
break;
}
}
}
return ret;
}
};
解法三:归并排序
我们知道归并排序就是将两个原本就有序的序列合并为一个有序的序列。如果两个序列长度都为1,那么它们当然就是有序的,我们将其合并为一个长度为2的有序序列。依此类推,我们就可以将一个乱序序列变为有序。而当前题目是要我们求一个乱序序列中各元素的右边所有元素中,小于该元素的元素的数量,我们该怎么利用归并排序来解决这个问题呢?
我们使用递归的方式实现自底向上的归并排序,在当前递归函数中,其左半部分和右半部分都是有序的(下级递归函数处理后返回到当前),那么我们就可以在将两部分合并的过程中,判断右边所有元素小于左边每一个元素的数量,然后再累加该数量(每个递归函数处理的是不同长度不同位置的元素)。为什么左边元素之间不需要比较呢?因为在之前的递归函数中已经比较了(所以现在才需要累加);为什么右边元素之间也不需要比较呢?也是因为在之前的函数中已经比较了。
为了实现该算法,我们需要定义一个数组index用来存储原数组中每个值得索引,这样我们才能根据值来找到其索引。
class Solution {
vector<int> count;
vector<int> index;
vector<int> temp;
public:
void merge(const vector<int> &nums, int lo, int mi, int hi) {
if (lo == mi || mi == hi) return;
//调用递归,自底向上
merge(nums, lo, (lo+mi) >> 1, mi);
merge(nums, mi, (mi+hi) >> 1, hi);
//临时数组为index腾出空间
for (int i = lo; i < hi; i++) {
temp[i] = index[i];
}
int p1 = lo, p2 = mi, p = lo;
//只要两边还有一边有剩余的就继续
while (p1 != mi || p2 != hi) {
if (p1 == mi) { //左边完了
index[p++] = temp[p2++];
} else if (p2 == hi) { //右边完了
index[p++] = temp[p1++];
count[index[p-1]] += (p2 - mi);//此时左边剩余元素都大于右边所有元素
} else if (nums[temp[p1]] > nums[temp[p2]]) { //当前左边元素大于右边元素,继续比较右边的下一个
index[p++] = temp[p2++];
} else { //直到左边当前元素不大于右边当前元素
index[p++] = temp[p1++];
count[index[p-1]] += (p2 - mi); //此时就可以将右边小于左边当前元素的个数累加起来了
}
}
}
vector<int> countSmaller(vector<int>& nums) {
int n = nums.size();
if (n == 0) return {};
if (n == 1) return {0};
temp.resize(n);
count.resize(n);
index.resize(n);
for (int i = 0; i < n; i++) {
index[i] = i;
count[i] = 0;
}
merge(nums, 0, n/2, n);
return count;
}
};
精简版
同样的思路但是没有索引数组而是使用迭代器,使用pair将数组中的值及其索引联系在一起,同时调用了inplace_merge库函数。
class Solution {
typedef vector<pair<int, int>> Pii;
typedef Pii::iterator Pit;
public:
vector<int> countSmaller(vector<int>& nums) {
int n = nums.size();
vector<int> res(n);
Pii nums_(n);
for(int i = 0; i < n; ++i)
nums_[i] = {nums[i], i};
merge(nums_.begin(), nums_.end(), res);
return res;
}
void merge(Pit begin, Pit end, vector<int>& res){
if(end - begin <= 1)
return;
auto mid = begin + (end - begin) / 2;
merge(begin, mid, res);
merge(mid, end, res);
for(auto i = begin, j = mid; i != mid; ++i){
while(j != end && i->first > j->first)
++j;
res[i->second] += j - mid;
}
inplace_merge(begin, mid, end);
}
};
同时有人提出归并排序是解决这种由索引及其值组成的pair的相关问题的很好的解法。在面试中我们使用归并排序解决问题往往会更简单,而使用BST、BIT等解法则是加分项。他甚至给出了这类问题的解决模板:
// [l, r) is the interval to be sorted
int sort_count(iterator l, iterator r) {
if (r - l <= 1) return;
// step 1. find the middle
iterator m = l + (r - l) / 2;
// step 2. sort left and right subarray
int count = sort_count(l, m) + sort_count(m, r);
/* step 3. write your code here for counting the pairs (i, j).*/
// step 4. call inplace_merge to merge
inplace_merge(l, m, r);
return count;
}
这道题目该有很多解法,不过最简单的也是大家最推荐的就是归并排序了。而其它算法大都实现起来十分庞杂,也很难在短时间想到,因此在面试过程中我们优先使用归并排序。其他的算法我这里就不一一分析了,这道题已经卡我好几天了。
题目十:Count of Range Sum
题目描述

题目给出一个整型数组和一个区间。要求我们找出该数组中所有可能连续元素之和在该区间的种数。连续元素最短就是一个元素本身,最长就是整个数组。
我的解法
题目要求我们的解决方案至少要优于$O(n^2)$,但是哪有那么简单,因此我就先简单实现$O(n^2)$的算法。虽然通过了全部case,但是很遗憾,太慢了,已经超出了时间限制。
该算法就是简单地计算 以每一个元素为起始的所有可能区间的和,统计其中符合题目要求的个数。
class Solution {
public:
int countRangeSum(vector<int>& nums, int lower, int upper) {
int count = 0;
for (int i = 0; i < nums.size(); i++) {
if (lower <= nums[i] && nums[i] <= upper) {
count++;
}
long sum = nums[i];
for (int j = i+1; j < nums.size(); j++) {
sum += nums[j];
if (lower <= sum && sum <= upper) {
count++;
}
}
}
return count;
}
};
他人解法
解法一:归并排序
你可能会惊讶这道题目怎么也可以用排序呢?刚开始我也打算用排序,可是考虑到索引与值的对应关系,又放弃了。该算法的主要关键点在于sum数组,使用sum[i]表示原数组前i个元素的和,如原数组是[1 2 3 4 5],那么sum数组就是[0 1 3 6 10 15]。但是该数组不一定是有序的,因为原数组中存在负数,因此排序才有上场的机会。那么如何判断一串连续的元素并且它们的和在区间[lower, upper]里面呢?
归并排序上场。采用自底向上的策略,所以,每次处理时左右两个序列都是有序的,此时我们再以左边序列为起点,右边序列为终点,找到所有起点到终点和在题目给出的区间的种数count,得到count后再merge合并两个序列,最后返回count
class Solution {
public:
int mergeSort(vector<long> &sum, int lower, int upper, int lo, int hi) {
if (hi - lo <= 1) return 0;
int count = 0;
int mid = lo + (hi - lo) / 2;
count = mergeSort(sum, lower, upper, lo, mid) + mergeSort(sum, lower, upper, mid, hi);
int right = mid, left = mid;
for (int i = lo; i < mid; i++) {
while (left < hi && sum[left] - sum[i] < lower) left++;
while (right < hi && sum[right] - sum[i] <= upper) right++;
count += right - left;
}
inplace_merge(sum.begin()+lo, sum.begin()+mid, sum.begin()+hi);
return count;
}
int countRangeSum(vector<int>& nums, int lower, int upper) {
int n = nums.size();
vector<long> sum(n + 1, 0);
for (int i = 0; i < n; i++) {
sum[i+1] = sum[i] + nums[i];
}
return mergeSort(sum, lower, upper, 0, n+1);
}
};
解法二:multiset
STL中容器set、map以及multiset和multimap底层实现都是红黑树。其中set和multiset基本相同,搜索、插入和移除操作都拥有对数复杂度,唯一不同的是set中没有或者说不允许出现重复元素,而multimap则允许含有重复元素。因而我们使用multiset来解决此题。
该算法还是基于累加和sum,及sum[i]表示了原数组nums前i个元素之和。这样我们就可以使用sum[i]-sum[j]来表示nums[j]+nums[j+1]+…+nums[i-1]了,即索引区间[j, i-1]。,根据题意得要求,我们要找出满足lower <= sum[i] - sum[j] <= upper的所有可能。那么我们对于每一个i来说,只要满足 sum[i]-upper <= sum[j] <= sum[i]-lower即可。现在我们就来找对于每一个i,符合以上条件的j有多少个,然后再累加起来。
很幸运,我们不用手动去找了,因为multiset已经帮我们实现了。由于multiset已经自动将元素排序,其方法lower_bound(num)返回容器中大于等于num的第一个元素位置,upper_bound(num)返回容器中第一个大于num的位置。因此我们就调用这两个方法来实现。
-
sums.lower_bound(sum - upper)表示返回sums中第一个大于等于sum - upper的位置;(满足以上条件的j的最小值)
- sums.upper_bound(sum - lower)表示返回sums中第一个大于sum - lower的位置。(满足以上条件的j的最大值+1)
- distance顾名思义就是计算两个迭代器的距离,可看作a-b
class Solution {
public:
int countRangeSum(vector<int>& nums, int lower, int upper) {
int ret = 0;
long sum = 0;
multiset<long> sums;
sums.insert(0);
//find all lower <= sum[i] - sum[j] <= upper
for (int i = 0; i < nums.size(); i++) {
sum += nums[i];
ret += distance(sums.lower_bound(sum - upper), sums.upper_bound(sum - lower));
sums.insert(sum);
}
return ret;
}
};
解法n
我不做了!太TMD难了!
做到这里我已经心有余而力不足了,这些排序的难题已经大大超出了我的能力范围,要是在面试中出一道这种题目我估计就完了。做了这几道hard级别的排序题目,我才知道我缺失的数据结构方面的知识以及对排序的认识都太多了。就比如说上面的解法multiset就是红黑树实现的,但是我却没有这方面的知识。以及还有人用BIT或者BST来做的,这些我都不太熟悉。总之,我要补的知识太多了!
