算法基础之渐进符号

zhyjc6于2020-03-02发布 约3143字·约6分钟 本文总阅读量次

一个算法在编程语言的翻译下，变成计算机可以执行的程序。而计算机执行该算法的程序需要一定的时间。该执行时间的长短受到很多方面因素的影响，与比如cpu处理速度、硬盘或内存速度以及处理数据的多少都有关系。

因此我们不能仅仅靠判断算法的程序执行时间来判断算法的快慢或好坏。那么我们应该怎么去衡量一个算法的好坏呢？

计算机硬件的影响是”死的“，而数据的量却是”活的“，即计算机性能的差异远不如数据量的多少的差异对程序执行时间带来的影响来的明显。如果待处理的数据量很小，那么我们就无法区分出好的算法和不好的算法，因此我们可以假设待处理数据的量特别大。

而当输入规模n足够大，此时我们可以忽略硬件差异带来的影响，仅仅关注当输入规模无限增加时，算法的运行时间是如何随着输入规模的变大而增加。

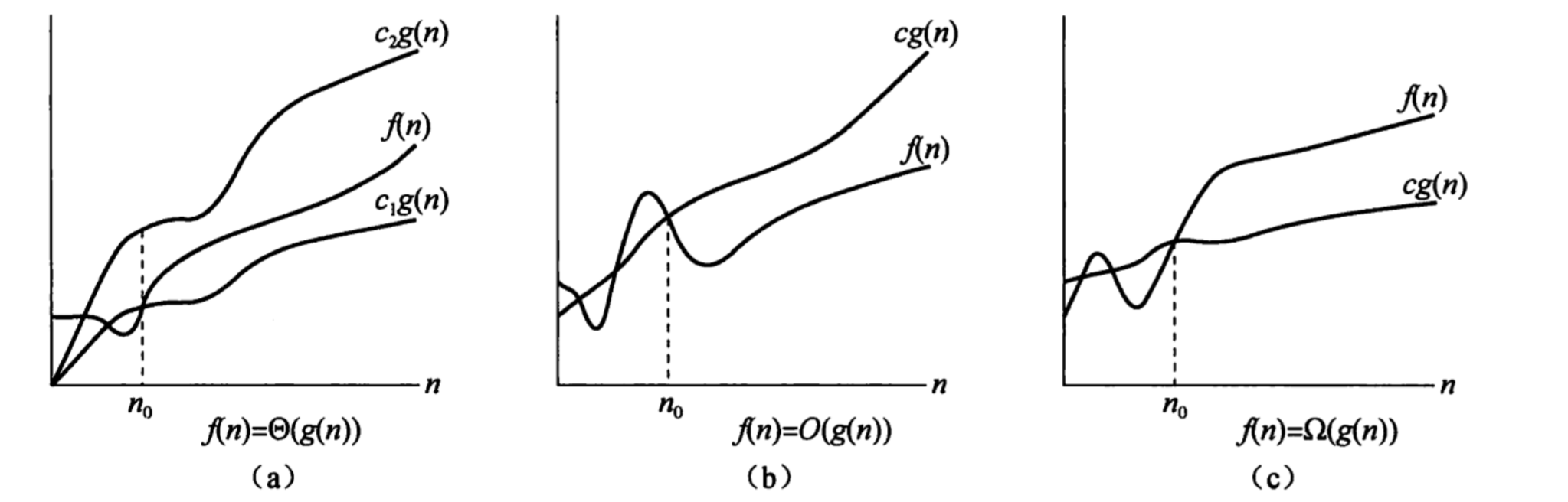
因此人们就定义了诸如$O,\Omega,\Theta$等渐进符号，下面是它们的图像描述。

$\Theta$记号

对一个给定的函数$g(n)$，用$\Theta(g(n))$来表示以下函数的集合：

意思是若存在正常量$c_1,c_2$，使得对于足够大的n，函数$f(n)$能”夹入“$c_1g(n)和c_2g(n)$之间，则$f(n)$属于集合$\Theta(g(n))$，因为$\Theta(g(n))$是一个集合，所以可以记为$f(n) \in \Theta(g(n))$，以指出$f(n)$是$\Theta(g(n))$的成员。但通常我们活用了等号，我们通常使用$f(n)=\Theta(g(n))$来表达相同的概念（这通常会使人产生误解,让我们忘记等号右边其实是一个集合，下同），如上图a，对所有$n>=n_0$，函数$f(n)$在一个常量因子内等于$g(n)$，我们称$g(n)$是$f(n)$的一个渐进紧确界(asymptotically tight bound)

O记号

$\Theta$记号渐进地给出一个函数的上下界，但当只有一个渐近上界时，使用$O$记号。

对于给定的函数$g(n)$，用$O(g(n))$来表示以下函数的集合：

我们使用O记号来给出函数的一个在常量因子内的上界，并且我们很容易得出$\Theta(g(n)) \subseteq O(g(n))$（类比于$[1,2]\in [-\infty,2]或者[1,2]\in [-\infty,6]等等$）

那么我们可不可以用$\Theta$代替$O$呢？为什么我们平时看到的都是$O$而不是$\Theta$呢？这是因为$\Theta$有上下限，已经把范围限定死了，而$O$是只有上界，包含的函数范围更广。例如插入排序的最坏情况运行时间是$\Theta(n^2)$，同时可以用$O(n^2)$表示，但当输入已经排好序时，插入排序的运行时间为$\Theta(n)$，但同样可以用$O(n^2)$表示。因此我们可以使用$O(n^2)$来表示整个算法所有情况（包含最好情况到最坏情况）的运行时间。

$\Omega$记号

与$O$相反，$\Omega$记号提供了渐进下界。对于给定的函数$g(n)$，用$\Omega(g(n))$来表示以下函数的集合：

上图c给出了$\Omega$记号的直观解释。由以上定义我们很容易推出以下定理：

定理：对任意两个函数f(n)和g(n)，我们有f(n)= $\Theta(g(n))$，当且仅当f(n)=$O(g(n))$且f(n)=$\Omega(g(n))$。

该定理很容易利用实数的例子来类比辅助理解：$x=y当且仅当x\le y且x \ge y$

我们知道插入排序的运行时间介于$\Theta(n)$和$\Theta(n^2)$，因为它落入n的线性函数与n的二次函数之间的任何地方。因此插入排序的时间不仅可以用$O(n^2)$来表示，还可以用$\Omega(n)$表示（个人理解）。

$o$记号

由$O$记号提供的渐进上界可能是也可能不是渐进紧确的，例如界$2n^2=O(n^2)$是渐进紧确的，但是界$2n=O(n^2)$却不是。我们使用$o$记号来表示一个非渐进紧确上界。

定义$o(g(n))$为以下集合：

例如，$n=o(n^2)$，但是$n^2\not=o(n^2)$

$\omega$记号

$\omega$记号与$\Omega$记号的关系类似于$o$记号与$O$记号的关系。我们使用$\omega$记号来表示一个非渐进紧确下界

定义$\omega(g(n))$为以下集合：

例如，$n^2=\omega(n)$，但是$n^2\not=\omega(n^2)$

渐进的性质

为了对渐进符号及其性质有一个更加直观的理解，我将每种渐进符号类比于实数：

$f(n)=O(g(n))$ 大概意思 $f(n)\le g(n)$

$f(n)=\Omega(g(n))$ 大概意思 $f(n)\ge g(n)$

$f(n)=\Theta(g(n))$ 大概意思 $f(n)=g(n)$

$f(n)=o(g(n))$ 大概意思 $f(n)<g(n)$

$f(n)=\omega(g(n))$ 大概意思 $f(n)>g(n)$

以上类比的大概意思都是基于渐进的比较，即输入规模n是大到一定规模的数值。下面我们来了解一下渐进符号的相关性质吧！

传递性

\(f(n)=\Theta(g(n))且g(n)=\Theta(h(n))\) \(蕴涵f(n)=\Theta(h(n))\)

$f(n)=O(g(n))且g(n)=O(h(n))$ $蕴涵f(n)=O(h(n))$

$f(n)=\Omega(g(n))且g(n)=\Omega(h(n))$ $蕴涵f(n)=\Omega(h(n))$

$f(n)=o(g(n))且g(n)=o(h(n))$ $蕴涵f(n)=o(h(n))$

$f(n)=\omega(g(n))且g(n)=\omega(h(n))$ $蕴涵f(n)=\omega(h(n))$

自反性

$f(n)=\Theta(f(n))$

$f(n)=O(f(n))$

$f(n)=\Omega(f(n))$

对称性

$f(n)=\Theta(g(n))当且仅当g(n)=\Theta(f(n))$

转置对称性

$f(n)=O(g(n))当且仅当g(n)=\Omega(f(n))$

$f(n)=o(g(n))当且仅当g(n)=\omega(f(n))$

三分性

对于任意两个实数a、b,下列3种情况必须恰有一种情况成立：

  1. a < b
  2. a = b
  3. a > b

然而对于函数而言，不是所有函数都能进行渐进比较，也就是说对于两个待比较函数$f(n)和g(n)$，也许$f(n)=O(g(n))和f(n)=\Omega(g(n))$都不成立

例如我们不能使用渐进记号来比较函数$n和n^{1+sin n}$，因为$n^{1+sin n}$的幂值在0到2之间摆动，取值为该范围内的所有值。

参考资料