牛顿迭代法

zhyjc6于2020-07-06发布 约2016字·约4分钟 本文总阅读量次

前言

今天在 leetcode 上刷题遇到一个简单题（69. x 的平方根），我也很快提交答案并通过。然后就去逛讨论区，看见评论区有人提出用牛顿迭代法，所以就有了这篇文章。

先看一下这题的题目描述吧：

题目只是简单的要求平方根，于是我写出了以下代码：

class Solution {
public:
    int mySqrt(int x) {
        int i;
        for (i = 1; i <= x/i; ++i) {
            if (i * i == x) return i;
        }
        return i-1;
    }
};

但是牛顿迭代法是这样：

class Solution {
public:
    int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }
        double x0 = x, x1 = x, C = x;
        while (1) { //f(x) = x*x - C, f'(x) = 2x
            x1 = x0 - (x0 * x0 - C) / (2 * x0); //可以继续优化：0.5 * (x0 + C / x0);
            if (x0 - x1 < 1e-6) {
                break;
            }
            x0 = x1;
        }
        return (int)x0;
    }
};

ok！看到这里发现牛顿迭代法是个好东西，一定要搞懂，于是找资料发现这个方法也有不少缺陷。

简介

背景

多数方程不存在求根公式，因此求精确根非常困难，甚至不可解，从而寻找方程的近似根就显得特别重要。方法使用函数 $f(x)$ 的泰勒级数的前面几项来寻找方程 $f(x)=0$ 的根。牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程 \(f(x)=0\) 的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根，此时线性收敛，但是可通过一些方法变成超线性收敛。另外该方法广泛用于计算机编程中。

公式

用牛顿迭代法解非线性方程，是把非线性方程 $f(x)=0$ 线性化的一种近似方法。把 $f(x)$ 在点 $x_0$ 的某邻域内展开成泰勒级数：

\[f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)(x-x_0)^2}{2!}+\cdots + \frac{f^n(x_0)(x-x_0)^n}{n!} + R_n(x)\]

取其线性部分（即泰勒展开的前两项），并令其等于0，即： \(f(x_0)+f'(x_0)(x-x_0)=0\) ，以此作为非线性方程 $f(x)=0$ 的近似方程，若 $f’(x_0) \ne 0$ ，则其解为：

\(x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}\) ，

这样，得到牛顿迭代法的一个迭代关系式：

\(x_{n+1}=x_n- \frac{f(x_n)}{f'(x_n)}\) 。

本质

牛顿迭代法的本质就是利用了切线是曲线的线性逼近的这一性质。

例如一个函数的曲线如下图所示，要求该函数的根：

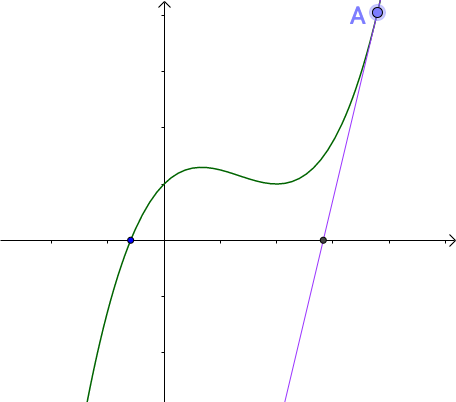
我们先随便找一个曲线上的点A（根据切线是切点附近的曲线的近似，应该在根点附近找，但是我们现在还不知道根点在哪里），做切线，切线与横坐标有个交点，这就是迭代一次的近似解。从该点做横坐标的垂线交曲线于点B，继续在B点做切线，然后再与横坐标有一个交点，这是迭代两次的近似解。

每次迭代可能会靠近真实的根，也可能会偏离真实的根。但绝大部分情况是，迭代次数足够多时，一定会无限接近真实的根。

不足

一、并不总是收敛(求得近似的根)

如果我们选择了函数的驻点作为起始点，那么得到的切线将与横坐标平行，也就无法再做下一条切线了。

二、越来越远离的不收敛

有些函数如 $f(x)=x^{\frac{1}{3}}$ ，不论我们怎么选择起始点，得到的近似根越迭代就越远离真实的根。

三、循环震荡的不收敛

有些函数如 $f(x)={\vert x \vert} ^\frac{1}{2}$ ，不论怎么选择起始点，得到的近似根是在左右不断震荡（跳转）的。

四、不能求出所有根

许多函数都有不止一个根，但是由于我们最终只能接近一个根，所以只能求出一个根。并且由于选择的起始点位置不同，得到的根也可能不同，这是不能确定的。

应用

求平方根还是很安全的，因为二次函数不论在哪个点做切线都会与横坐标有交点。

例如我们求自然数 C 的平方根，就将其看作 $x^2 - C = 0$ ，再用牛顿迭代法求该方程的根。由于我们已经确定 $-C < x^2 < C$ ，所以我们可以将 C 视为起始点，逐步向根逼近。

参考