题目一:Clone Graph
题目描述
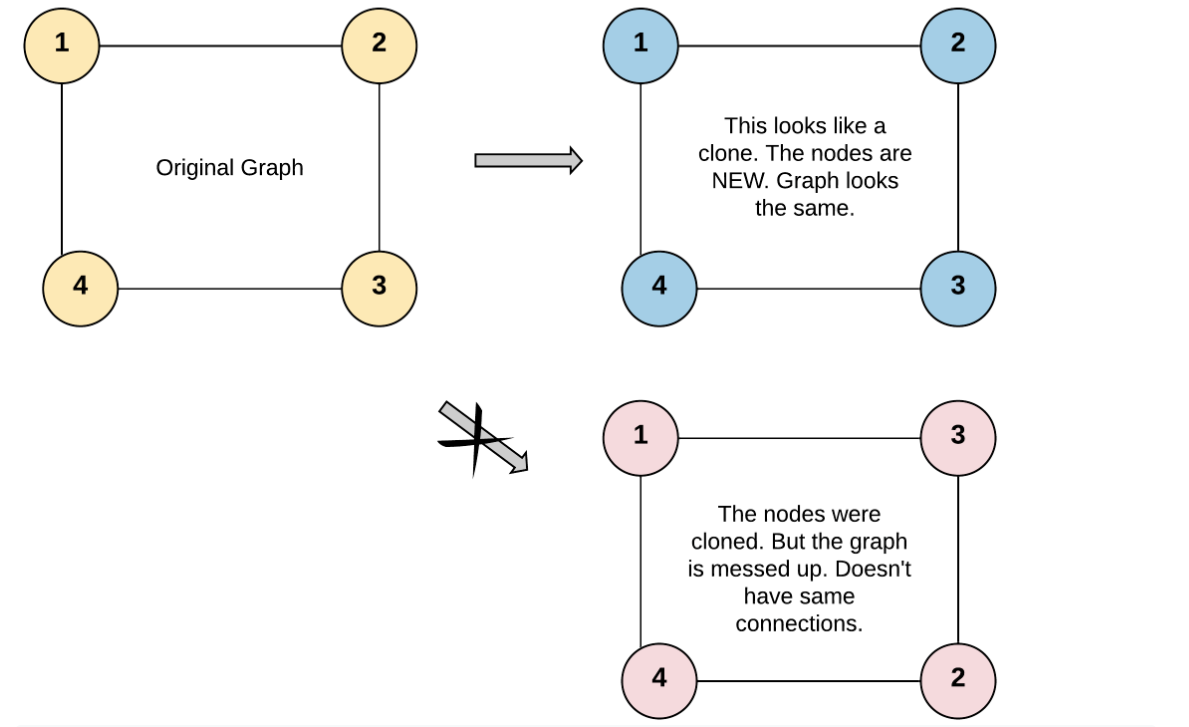
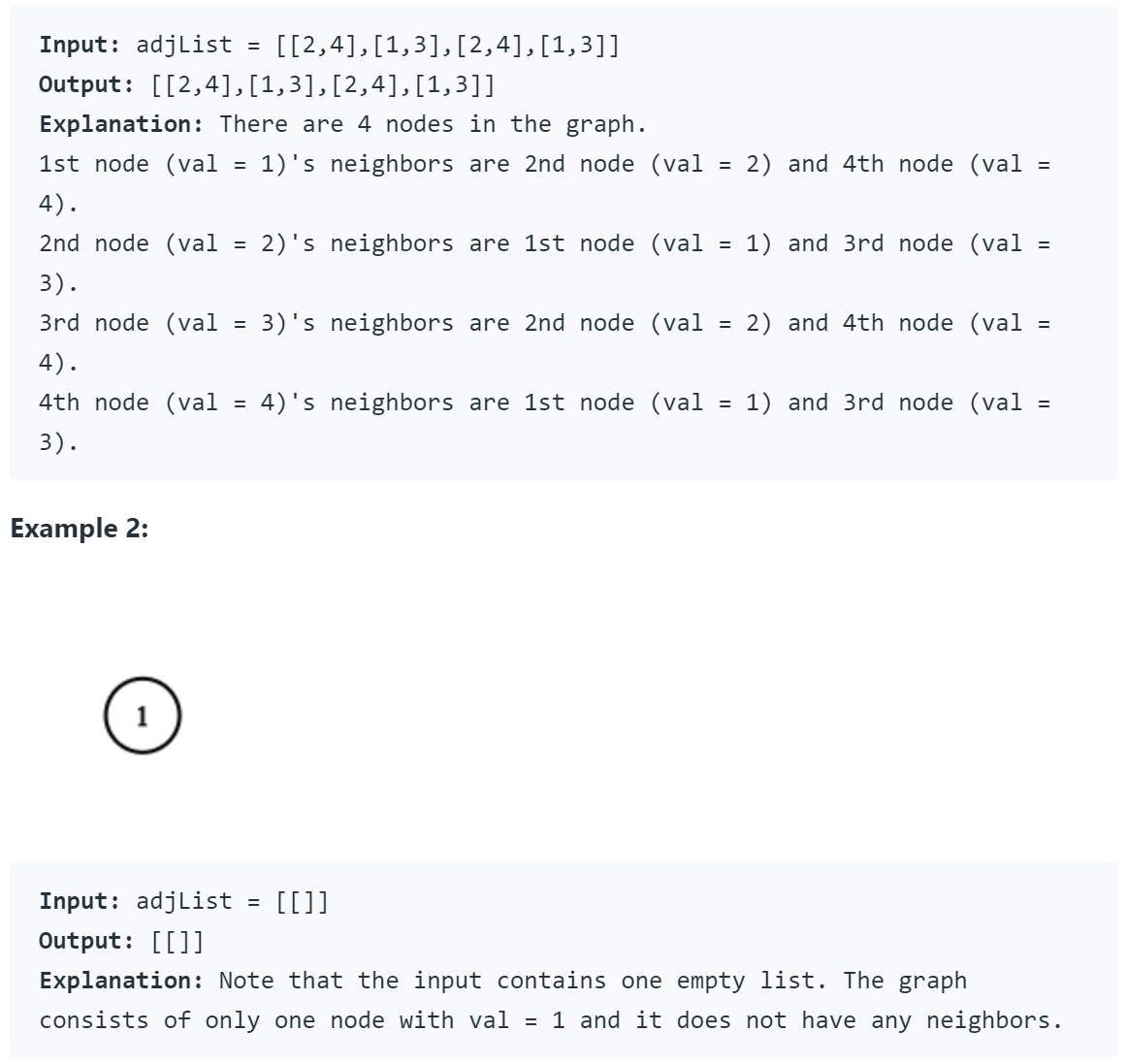
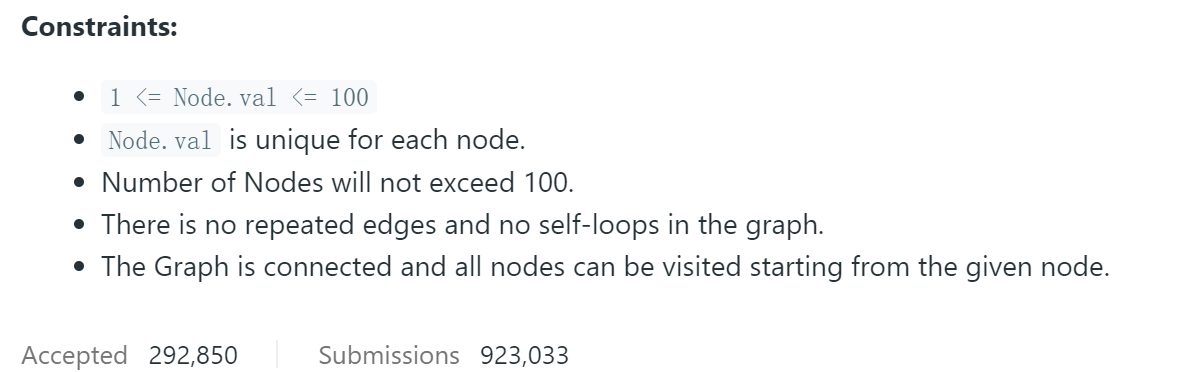
题目描述是真的长啊!不过意思很简单,就是要我们深度复制一张图,图的结点结构已经告诉我们了,同时还约定了每张图的结点数都不超过100,图中没有重复的边和结点,没有结点指向自己,所有结点都可以访问到。其中每个结点的结点值用整数$x$表示($x\in [1,100]$)。
我的解法
初次做到图的题目,还是有一点棘手。之前也经常听说过常见的图的遍历,如深度优先遍历和广度优先遍历等。我在想要复制一张图,那肯定得遍历整张图吧!而不管采用什么方式遍历一张图,由于图中没有一个确切的终点(不像树那样可以通过子结点判断),因此我们必须额外定义一个数组,来表示对应的结点是否被访问过。
起初我是打算使用vector(n+1, false)来表示的,但是我们又不能事先知道图中有多少结点,因此这个方法不行。然后我又想到使用map(node->val, false/true) 以及map(node_val, node)来表示,但是都没有成功。
他人解法
解法一:DFS
使用map<Node*, Node*>的数据结构直接构造每一个结点的邻居,最后返回题目给出的当前结点就好了。
map的作用有两个:
- 判断结点是否访问过
- 建立旧的图和新的图之间的联系:
map[*old_node] = *new_node
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> neighbors;
Node() {
val = 0;
neighbors = vector<Node*>();
}
Node(int _val) {
val = _val;
neighbors = vector<Node*>();
}
Node(int _val, vector<Node*> _neighbors) {
val = _val;
neighbors = _neighbors;
}
};
*/
class Solution {
public:
map<Node*, Node*> clone;
Node* cloneGraph(Node* node) {
if (!node) return nullptr;
if (clone.find(node) == clone.end()) {
clone[node] = new Node(node->val);
for (Node* neighbor : node->neighbors) {
clone[node]->neighbors.push_back(cloneGraph(neighbor));
}
}
return clone[node];
}
};
解法二:BFS
与树的广度优先遍历搜索一样,图的BFS也是基于队列的迭代法。
首先把node复制并放入map中,再将其放入队尾,如果队列不为空,则每次从队首取出一个结点来处理,遍历该结点的每一个邻居,如果其某一邻居没有遍历过,复制邻居结点并放入map,然后再将其放入队尾等待处理,最后再在map中当前结点的邻居列表里插入复制的邻居;如果该邻居是遍历过(map中找得到)的,则直接在map中当前结点的邻居列表里插入复制的邻居。继续从队首取出一个结点来处理,重复以上步骤直到队列为空,表示没有未遍历的结点了。
map的作用同解法一。
class Solution {
public:
Node* cloneGraph(Node* node) {
if (!node) {
return NULL;
}
Node* copy = new Node(node -> val, {});
copies[node] = copy;
queue<Node*> todo;
todo.push(node);
while (!todo.empty()) {
Node* cur = todo.front();
todo.pop();
for (Node* neighbor : cur -> neighbors) {
if (copies.find(neighbor) == copies.end()) {
copies[neighbor] = new Node(neighbor -> val, {});
todo.push(neighbor);
}
copies[cur] -> neighbors.push_back(copies[neighbor]);
}
}
return copy; //copies[node]
}
private:
unordered_map<Node*, Node*> copies;
};
题目二:Course Schedule
题目描述
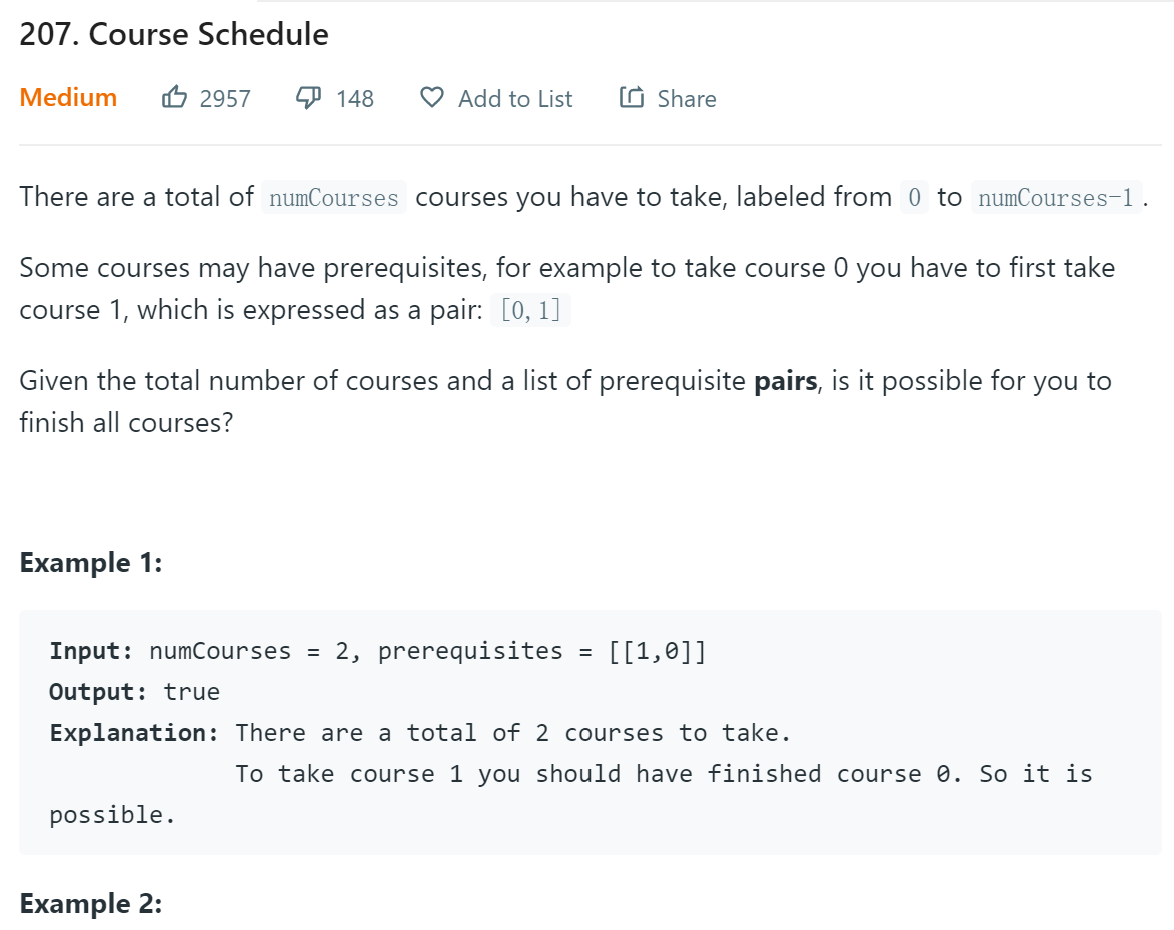
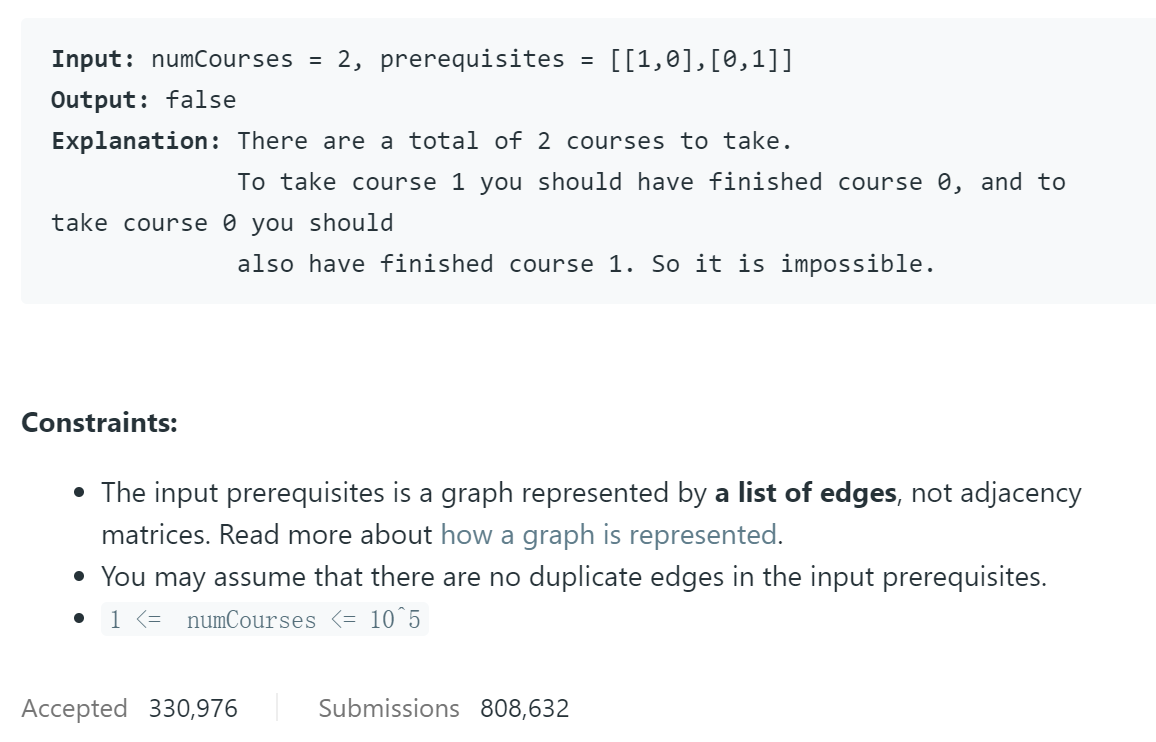
题目给出一些课程,要求我们判断我们能不能学完。你可能会觉得有些疑惑,一直上课不就能学完了嘛。但是有些课程有先修课程,如果该课程的先修课程,先修课的先修课。。。最终连接到该课程,那么我们就不能学完了。例如1的先修课程是2,2的先修课程是1。这时候我们就不能学完课程1和2。
我的解法
刚开始不会。拖了两天去看了别人的解法,才知道。
该题目给出的课程其实组成的是一张有向图,而能不能学完这些课程关键就在于有向图中是否有环存在。而该题本质上就是拓扑排序,拓扑排序原理: 对 DAG 的顶点进行排序,使得对每一条有向边 $(u, v)$,均有 $u$(在排序记录中)比 $v$ 先出现。亦可理解为对某点 $v$ 而言,只有当 $v$ 的所有源点均出现了,$v$ 才能出现。
使用二维数组graph来表示有向图,一维数组in来表示每个结点的入度。我们一开始根据给出的课程建立有向图并初始化数组in。然后我们定义一个队列,将所有入度为0的结点放入队列中。然后我们再循环遍历队列,取出队首结点,并将其指向的所有结点的入度减1,如果此时有结点入度为0,那么将其加入队尾。直到队列为空,此时我们再遍历一遍入度数组in,如果还有结点入度不为0,那么就说明原有向图中有环存在,返回false,否则就是有向无环图,返回true。
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
queue<int> q;
vector<int> in(numCourses);
vector<vector<int>> graph(numCourses, vector<int>());
//build directed graph and initial in
for (auto a : prerequisites) {
graph[a[1]].push_back(a[0]);
in[a[0]]++;
}
//push all nodes that in-degree is 0
for (int i = 0; i < numCourses; i++) {
if (in[i] == 0) {
q.push(i);
}
}
while (!q.empty()) {
int zeroNode = q.front();
q.pop();
for (int newNode : graph[zeroNode]) {
in[newNode]--;
if (in[newNode] == 0) {
q.push(newNode);
}
}
}
for (auto i : in) {
if (i != 0) {
return false;
}
}
return true;
}
};
他人解法
解法一:BFS
原理和我们上面的解法一样,区别就在于最后队列为空后,我们不需要遍历数组in来判断入度是否全部为0。
若整个课程安排图是有向无环图(即可以安排),则所有节点一定都入队并出队过,即完成拓扑排序。因此,拓扑排序出队次数等于课程个数就是有向无环图(可以安排)。我们只需要在每次pop之后numCourses–,最后返回 numCourses == 0 就可以判断课程是否可以成功安排。
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
queue<int> q;
vector<int> in(numCourses);
vector<vector<int>> graph(numCourses, vector<int>());
//build directed graph and initial in
for (auto a : prerequisites) {
graph[a[1]].push_back(a[0]);
in[a[0]]++;
}
//push all nodes that in-degree is 0
for (int i = 0; i < numCourses; i++) {
if (in[i] == 0) {
q.push(i);
}
}
while (!q.empty()) {
int zeroNode = q.front();
q.pop();
numCourses--;
for (int newNode : graph[zeroNode]) {
in[newNode]--;
if (in[newNode] == 0) {
q.push(newNode);
}
}
}
return numCourses == 0;
}
};
- 时间复杂度 $O(N + M)$: 遍历一个图需要访问所有节点和所有临边,$N$ 和 $M$ 分别为节点数量和临边数量;
- 空间复杂度 $O(N + M)$: 为建立邻接表所需额外空间,adjacency 长度为 $N$ ,并存储 $M$ 条临边的数据。
解法二:DFS
我们知道上面的BFS遍历是每个结点只遍历一遍,为了提高效率,我们的DFS也要达到每个结点只遍历一遍的效果。那么如何实现呢?这里我们需要给每个结点定义一个flag,如果flag = 0,说明该结点从来没有遍历过;如果flag = -1,那么说明该结点在其它结点调起的DFS中被访问过,不可能构成环,因此我们直接返回true;如果flag = 1,说明该结点在当前DFS中已经遍历过,现在是2次遍历,说明存在环,直接返回false。
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
vector<vector<int>> graph(numCourses, vector<int>());
vector<int> flags(numCourses, 0);
for (auto courses : prerequisites) {
graph[courses[1]].push_back(courses[0]);
}
for (int i = 0; i < numCourses; i++) {
if (DFS(graph, flags, i) == false) {
return false;
}
}
return true;
}
bool DFS(vector<vector<int>> &graph, vector<int> &flags, int node) {
if (flags[node] == -1) return true;
if (flags[node] == 1) return false;
flags[node] = 1;
for (int nodei : graph[node]) {
if (DFS(graph, flags, nodei) == false) {
return false;
}
}
flags[node] = -1;
return true;
}
};
题目三:Course Schedule II
题目描述
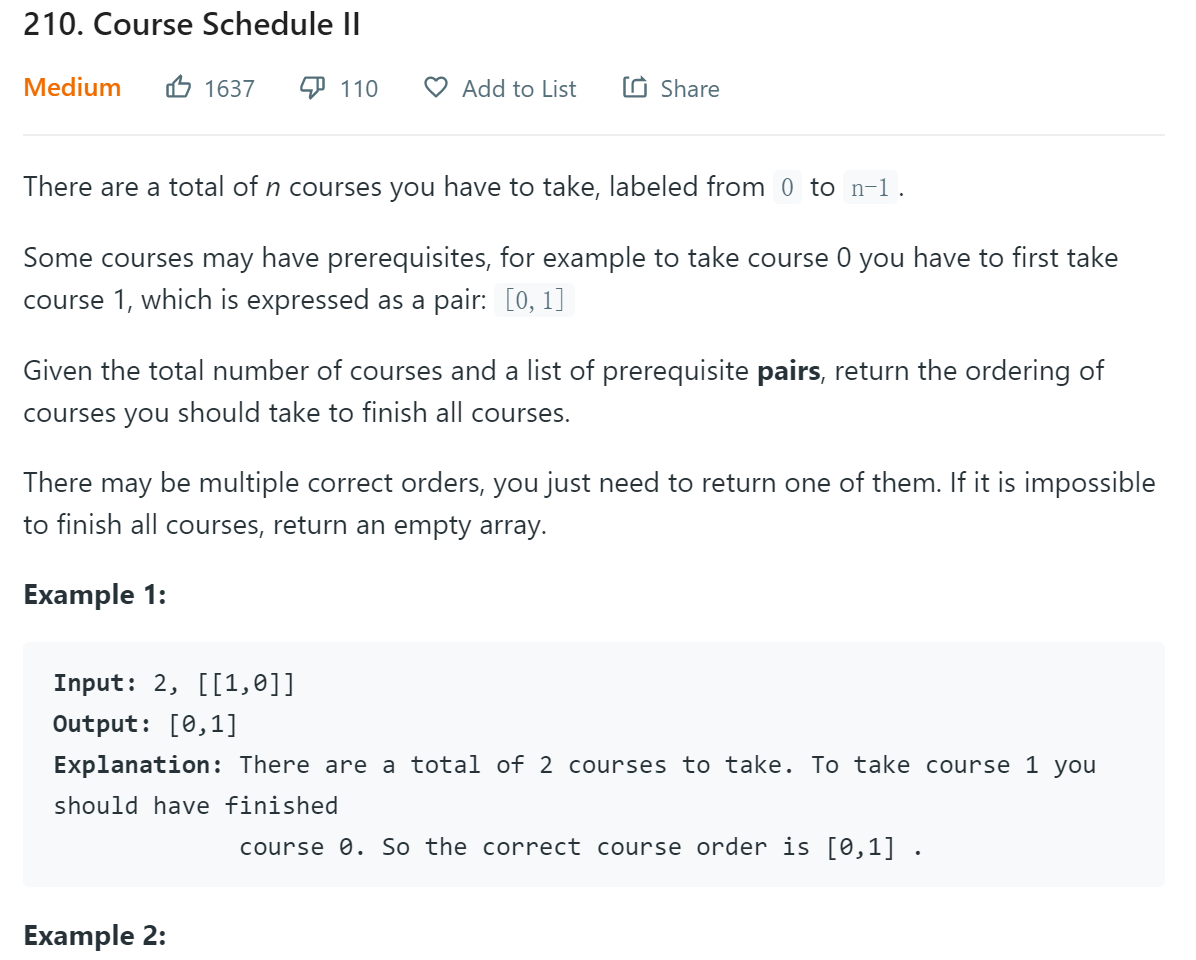
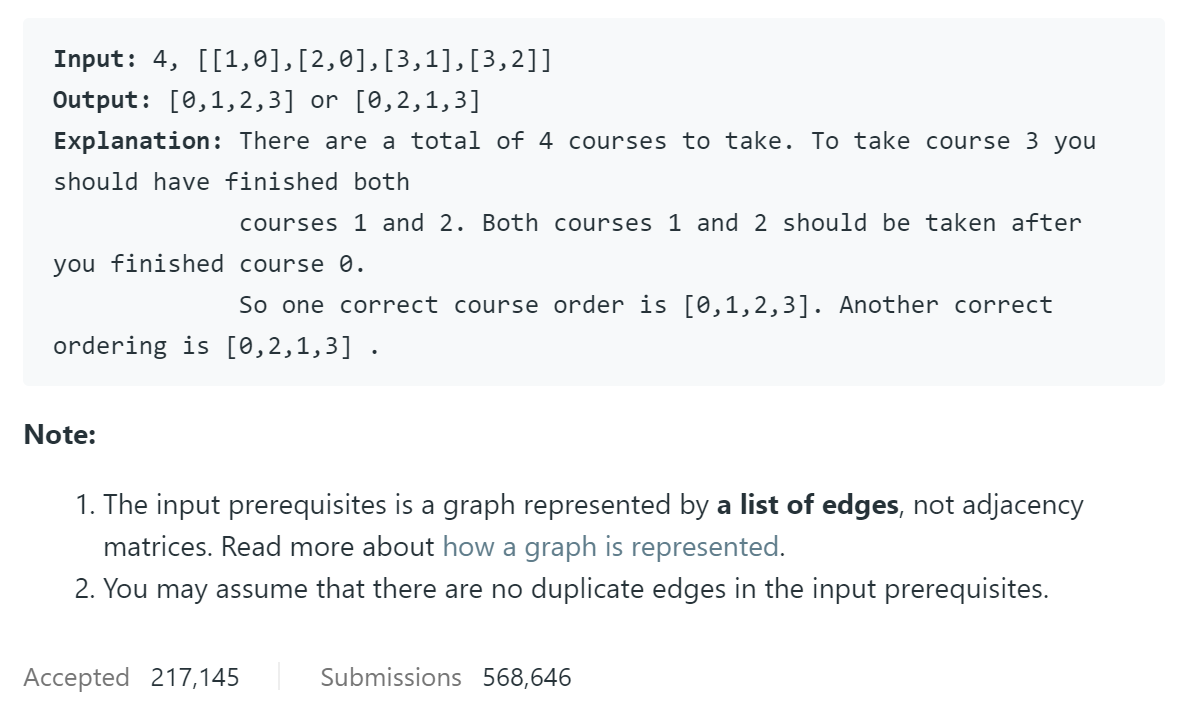
给出一堆课,其中某些课是另一些课的先修课程,要求我们得到一个课程顺序使得课程可以按顺序学完。其实就是上一题的进一步要求,我们只需要把DFS或BFS遍历过程中的课程一个个打印出来就好了。
我的解法
有了上一题的经验,这次我使用BFS那是信手拈来,一下子就通过了。不同的地方就是多定义了一个数组ret,每次队列弹出队首元素就将其放入ret,最后再判断数组ret的元素个数是否为numCourses,如果是的话就返回ret,否则就说明有环,无法完成所有课程,这时我们直接返回{}
class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<vector<int>> graph(numCourses, vector<int>());
vector<int> in(numCourses, 0);
queue<int> q;
vector<int> ret;
for (auto edge : prerequisites) {
graph[edge[1]].push_back(edge[0]);
in[edge[0]]++;
}
for (int i = 0; i < numCourses; i++) {
if (in[i] == 0) {
q.push(i);
}
}
while (!q.empty()) {
int cur = q.front();
q.pop();
ret.push_back(cur);
for (int next : graph[cur]) {
in[next]--;
if (in[next] == 0) {
q.push(next);
}
}
}
if (ret.size() < numCourses) {
return {};
}
return ret;
}
};
他人解法
DFS
采用邻接链表建立表,以每一个结点为起始结点,深度优先递归遍历判断是否有环,如果有环则判断无法完成,返回空集;否则把当前遍历过的结点标记为已遍历结点(flags[i] = -1),再继续以下个结点(如上一个是i,这一个就是i+1)为起始结点递归遍历找环,如果遍历到当前正在遍历的结点(flags[i] = 1),那么说明有环,返回空集;如果遍历到之前几轮遍历过的结点(flags[i] = -1),说明无环,继续下一轮遍历;否则(flags[i] = 0)继续递归,如此循环直到遍历完所有结点。
注意:这里我们需要将递归函数使用传引用的方式传递参数,因为传值的方式在每次递归调用的过程中都会复制一个相同的参数在当前栈帧中,而我们的参数graph又是个占用内存极大的变量。因此每次的递归调用复制参数都会花费很长时间。因此我们如果使用传值的方式会超出时间限制,而传引用的方式就不用复制整个graph内存,而是直接为其建立一个引用,也就是一个指针,传递效率大大提高。
class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
vector<vector<int>> graph(numCourses, vector<int>());
vector<int> flags(numCourses, 0);
vector<int> order;
for (auto edge : prerequisites) {
graph[edge[1]].push_back(edge[0]);
}
for (int i = 0; i < numCourses; i++) {
if (!DFS(graph, flags, order, i)) {
return {};
}
}
reverse(order.begin(), order.end());
return order;
}
private:
bool DFS(vector<vector<int>> &graph, vector<int> &flags, vector<int> &order, int cur) {
if (flags[cur] == 1) return false;
if (flags[cur] == -1) return true;
flags[cur] = 1;
for (int next : graph[cur]) {
if (!DFS(graph, flags, order, next)) {
return false;
}
}
order.push_back(cur);
flags[cur] = -1;
return true;
}
};
题目四:Minimum Height Trees
题目描述


题目给出一张无向图(一个整数n代表0、1、2…、n-1这n个结点,一个二维数组edges表示图中的每一条边),并指示图中没有重复的边,没有环(如果有环就不能构成树了),要求我们在图能构成的所有树中找到高度最小的树,并返回这些树的根结点。
我的解法
暴力DFS
无向图中没有环,那么要构成树就很简单,只需要以任意结点为根结点,把它“拎”起来就构成了一棵树。而一棵树的高度是其根结点到叶结点的最远距离。因此一开始我打算遍历所有结点,以其为根结点构造树,在得到的所有树中在选取高度最小的那几棵(最多两棵树,下面会说)。
我为了简单使用了递归实现,但是过程坎坷,尽管最终还是实现了。该算法在最后一个case时超出了时间限制,看起来确实不够高效。
虽然该算法效率较低,但我还是对其进行了优化:
- 剪枝处理:叶子节点直接跳过,因为叶子结点为根结点构成的树的高度一定大于中间结点构成的树的高度
- 递归函数传引用,这是我吸取了上一题的经验
class Solution {
public:
int max_depth;
vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
vector<vector<int>> graph(n, vector<int>());
vector<int> len(n, INT_MAX);
vector<int> res;
for (auto edge : edges) {
graph[edge[0]].push_back(edge[1]);
graph[edge[1]].push_back(edge[0]);
}
for (int i = 0; i < n; i++) {
if (graph[i].size() == 1) {
continue;//叶子结点可以直接跳过
}
max_depth = 0;
DFS(graph, i, 1, -1);
len[i] = max_depth;
}
int mindepth = *min_element(len.begin(), len.end());
for (int i = 0; i < len.size(); i++) {
if (len[i] == mindepth) {
res.push_back(i);
}
}
return res;
}
void DFS(vector<vector<int>> &graph, int root, int depth, int lastroot) {
if (graph[root].size() == 1) {
max_depth = max(max_depth, depth);
return;
}
for (int nei : graph[root]) {
if (nei != lastroot) {
DFS(graph, nei, depth+1, root);
}
}
}
};
他人解法
解法一:剥洋葱
题目只需要我们求出该图构成的树中高度最小的树的根结点,那么我们可以从图的外围开始,像剥洋葱一样一层一层把叶子结点剥掉,直到最后只剩一个或两个结点就是答案。为什么是一个或两个呢?因为图中没有环,如果有三个或以上,我们还可以继续“剥洋葱”,而如果只有一两个我们就不能继续剥了。
具体的实现有点类似于拓扑排序,就是:
- 找到所有叶子结点(度为1)
- 在图中删除这些结点及其邻边
- 重复以上过程直到只剩下一个或两个结点
class Solution {
public:
int max_depth;
vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
if (n == 1) return {0};
vector<unordered_set<int>> graph(n);
queue<int> leaves;
vector<int> ret;
for (auto edge : edges) {
graph[edge[0]].insert(edge[1]);
graph[edge[1]].insert(edge[0]);
}
for (int i = 0; i < n; i++) {
if (graph[i].size() == 1) {
leaves.push(i);
}
}
while (n > 2) {
int size = leaves.size();
n -= size;
for (int i = 0; i < size; i++) {
int leaf = leaves.front();
leaves.pop();
for (auto nei : graph[leaf]) {
graph[nei].erase(leaf);
if (graph[nei].size() == 1) {
leaves.push(nei);
}
}
}
}
while (!leaves.empty()) {
ret.push_back(leaves.front());
leaves.pop();
}
return ret;
}
};
解法二:树的直径
根据算法导论第三版第22章课后题22.2-8的定义:
我们将一棵树$T=(V,E)$的直径定义为$max_{u,v\in V}\delta(u,v)$,也就是说,树中所有最短路径的最大值即为树的直径。
换句话说,树中距离最远的两个结点之间的距离就是直径。在这里我们也可以将其理解为连通无向无环图的直径。如果我们找到题目中图的直径,那么直径的中点(可能是一个或两个结点)就是我们要求的结果。
算法很简单,我们以图中任意结点x为起点,找到距离其最远的结点y,此时y一定是图中某一条直径(可能会有多条直径,但直径的中点一定不变,即直径相交于中点)的一端,那么我们以y为起点,找到距离其最远的结点z,此时z一定是y所在直径的另一端,即(y,z)为一条直径。
怎么证明上面的算法是正确的呢?参考文章:树的直径

算法很简单,证明也有了,现在我们来具体实现:
class Solution {
public:
int max_len;
int v;
vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
vector<vector<int> > graph(n);
vector<bool> visited(n,false);
vector<int> path;
vector<int> res;
for(int i = 0 ; i < edges.size(); i++){
graph[edges[i][0]].push_back(edges[i][1]);
graph[edges[i][1]].push_back(edges[i][0]);
}
dfs(graph,visited,0,0,path);
max_len = 0;
path.clear();
dfs(graph,visited,v,0,path);
if(max_len % 2 == 0){
res.push_back(path[max_len/2]);
res.push_back(path[max_len/2-1]);
}
else{
res.push_back(path[max_len/2]);
}
return res;
}
void dfs(vector<vector<int>>& graph, vector<bool>& visited, int i, int count, vector<int>& path){
visited[i] = true;
count++;
path.push_back(i);
for(auto it = graph[i].begin(); it != graph[i].end(); it++){
if(!visited[*it]){
dfs(graph,visited,*it,count,path);
}
}
if(count > max_len){
max_len = count;
v = i;
}
visited[i] = false;
}
};
题目五:Reconstruct Itinerary
题目描述
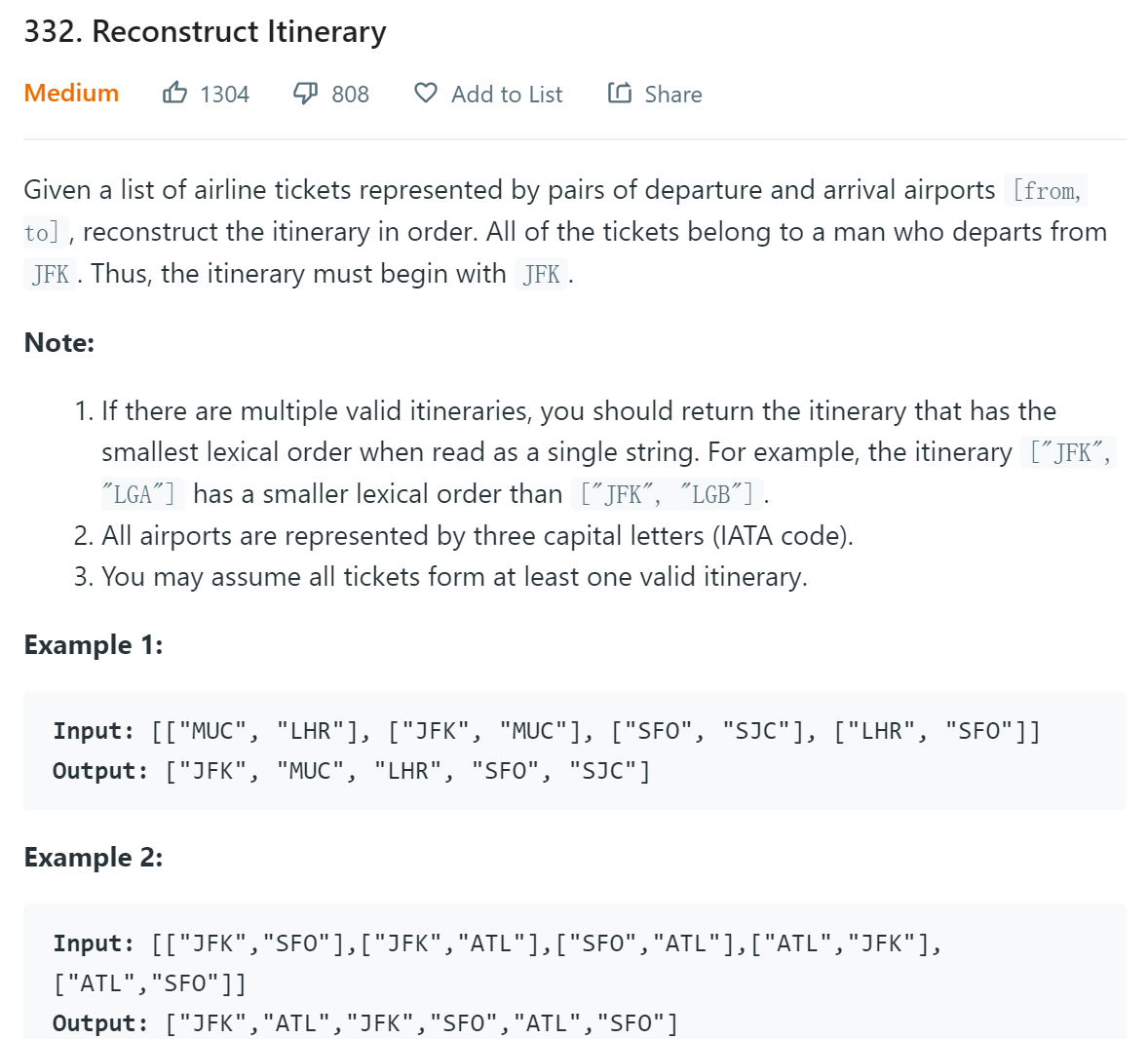

题目给出一组机票集合和一个固定起点(”JFK”),要求我们以最小字典序给出一个机票规划路线。
我的解法
错误解法
我刚开始看到例题以为就是简单将机票首尾拼接起来,最多给排个序就好了。于是我使用了map和优先队列,以邻接链表的方式构建了一个有向图,我的思路就很简单了,以起点为当前机场,在有向图中找到该机场并返回该机场对应的优先队列中的队首机场,更新当前机场为队首机场,并弹出队首机场。再继续以当前机场在有向图中寻找其下一个机场,直到遇到优先队列为空,则返回。
我的代码:
class Solution {
public:
vector<string> findItinerary(vector<vector<string>>& tickets) {
map<string, priority_queue<string, vector<string>,greater<string>>> map;
vector<string> ret;
for (vector<string> s : tickets) {
map[s[0]].push(s[1]);
}
string cur = "JFK", next = "", end = "";
ret.push_back(cur);
while (true) {
if (map[cur].empty()) {
break;
}
next = map[cur].top();
map[cur].pop();
if (map.find(next) == map.end()) {
end = next;
continue;
}
ret.push_back(next);
cur = next;
}
if (end != "") {
ret.push_back(end);
}
return ret;
}
};
上述算法的问题在于,在当前机场寻找其下一个机场时,仅仅是基于简单的字典排序判断,而没有考虑到能不能顺利遍历全部机票。因此结果往往是漏掉了一些机票。
他人解法
解法一:递归
而递归算法就不一样了。如果忽略掉字典排序这一条件,那么这道题目的本质就是求有向图的欧拉路径,即从某一个点出发,按照有向图的方向不重复地遍历有向图中的每一条边。该点题目已经给出,就是机场“JFK”,而边就是题目给出的一张张机票。
我们递归调用的前提是建立有向图,这里我们使用优先队列作为邻接链表的实现,这样就不用我们自己实现字典排序了。递归调用的过程是深度优先遍历,每次去优先队列的队首并弹出队首,每次遇到优先队列为空,就顺序加入ret字符串数组,易知最后加入的一定是起点机场,那么反过来第一个加入的一定就是终点机场了(除了起点和终点,其它的点的出度等于入度,也就是有偶数条边,起点出度=入度+1,终点入度=出度+1),因此最后所有的优先队列都为空,所有的栈都已经弹出,那么我们将ret字符串数组翻转就是答案了。
下图参考:https://leetcode-cn.com/problems/reconstruct-itinerary/solution/javadfsjie-fa-by-pwrliang/
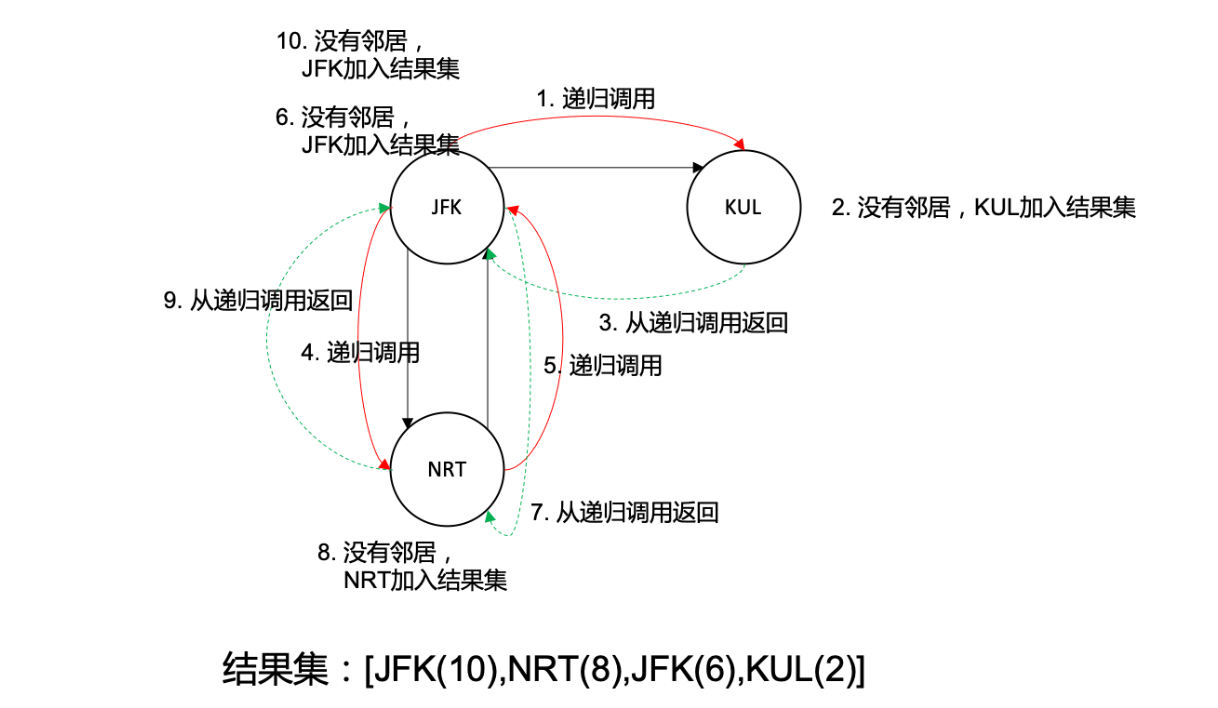
class Solution {
public:
unordered_map<string, priority_queue<string, vector<string>,greater<string>>> map;
vector<string> ret;
vector<string> findItinerary(vector<vector<string>>& tickets) {
for (auto ticket : tickets) {
map[ticket[0]].push(ticket[1]);
}
dfs("JFK");
reverse(ret.begin(), ret.end());
return ret;
}
void dfs(string airport) {
auto &airports = map[airport];
while (!airports.empty()) {
string next = airports.top();
airports.pop();
dfs(next);
}
ret.push_back(airport);
}
};
解法二:迭代法
我们应该知道,递归大致就等于迭代+栈,因此同样的思路,我们在栈的帮助下使用迭代也可以实现。
class Solution {
public:
unordered_map<string, priority_queue<string, vector<string>,greater<string>>> map;
stack<string> st;
vector<string> ret;
vector<string> findItinerary(vector<vector<string>>& tickets) {
for (auto ticket : tickets) {
map[ticket[0]].push(ticket[1]);
}
st.push("JFK");
while (!st.empty()) {
string cur = st.top();
if (map[cur].empty()) {
ret.push_back(cur);
st.pop();
} else {
st.push(map[cur].top());
map[cur].pop();
}
}
reverse(ret.begin(), ret.end());
return ret;
}
};
题目六:Evaluate Division
题目描述
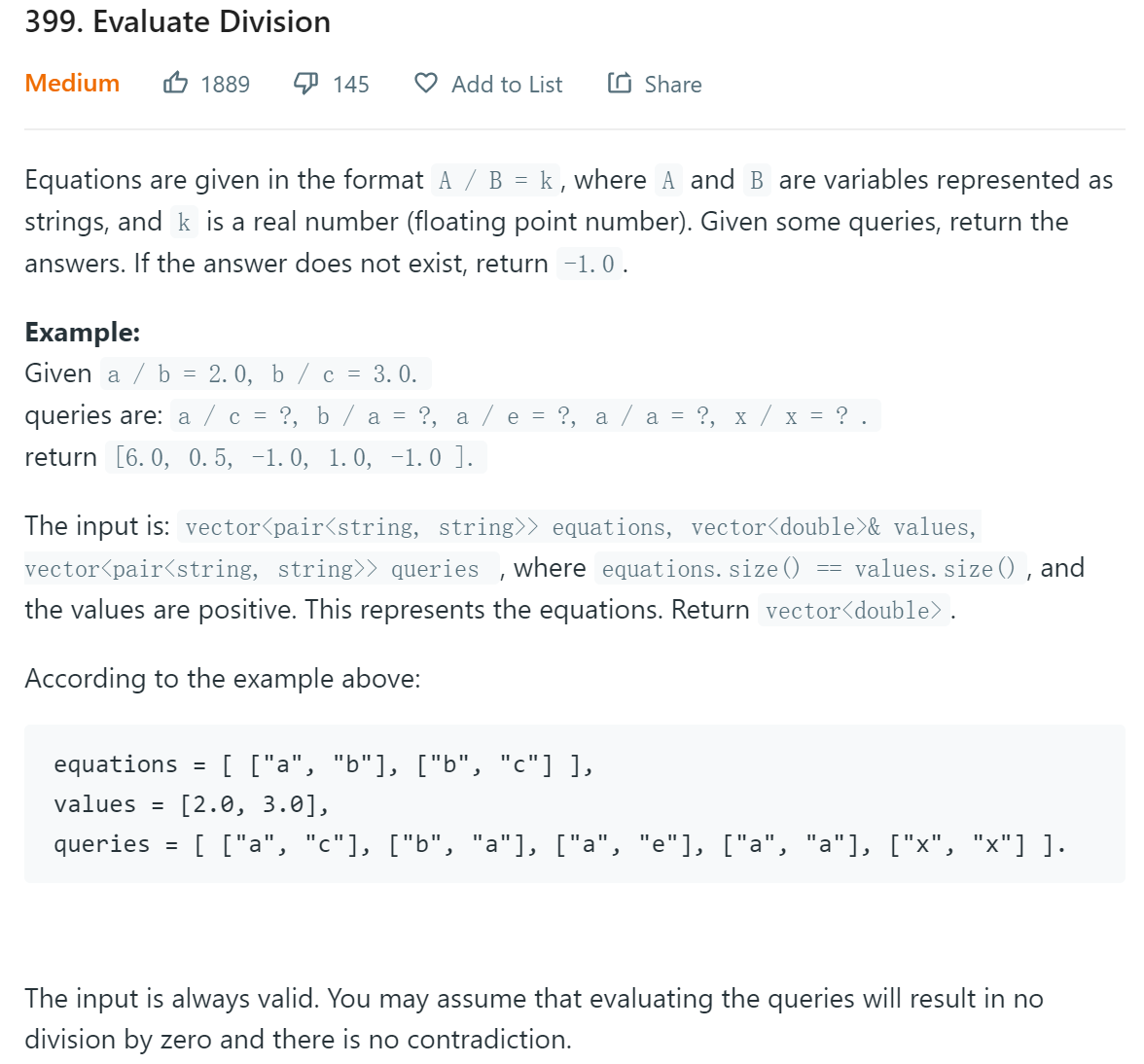

题目给出一组除法的等式和一组待求商的除法式子,要求我们求出这些商。其中等式的右边是统一的浮点数,等式左边的被除数和除数都是一些字符串,而除法式子中的被除数和除数也是同样的字符串,题目要求我们从等式中推断字符串之间的除法关系。如给出等式 "a" / "b" = 2.0, "b" / "c" = 3.0, 求"a" / "c" = ?
如果式子中的字符串在等式中没有出现,那么我们直接返回-1.0,如果都出现了但是被除数等于除数,那么我们返回1.0
我的解法
他人解法
解法一:BFS
采用邻接链表的方式构造双向有权图,如"a" / "b" = 2.0,那么我们就构造a -> b,边的权值为2.0,同时构造b -> a,边的权值为1.0/2.0 = 0.5。此时我们要求a / b = ?,只需要在双向图中以a为起点,b为终点,将一路上的边的权值乘起来,就得到了答案。为了方便我们构造一个函数answer
函数中采用队列来辅助,从而实现BFS。注意,这里我们可能会有多条路径能从a到达b,但是我们选取的不一定是最短路径,不过这没关系,因为不论路径长短,权值的积都是相等的。
class Solution {
public:
unordered_map<string, vector<pair<string, double>> > map;
vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
int n = equations.size();
vector<double> ret;
// 构造双向带权图
for (int i = 0; i < n; i++) {
map[equations[i][0]].push_back({equations[i][1], values[i]});
map[equations[i][1]].push_back({equations[i][0], 1.0/values[i]});
}
for (auto query : queries) {
ret.push_back(answer(query[0], query[1]));
}
return ret;
}
double answer(string a, string b) {
if (map.find(a) == map.end() || map.find(b) == map.end()) {
return -1.0;
}
if (a == b) {
return 1.0;
}
unordered_map<string, bool> visited(false);
visited[a] = true;
queue<pair<string, double>> q;
q.push({a, 1.0}); //起点
while (!q.empty()) {
auto cur = q.front();
q.pop();
visited[cur.first] = true;
for (auto &next : map[cur.first]) {
if (visited[next.first] == true) {
continue;
}
if (next.first == b) {
return cur.second * next.second; //终点
}
q.push({next.first, cur.second * next.second});
}
}
return -1.0;
}
};
解法二:打表
和上面算法一样,首先构造双向带权图,然后连接所有能连通的结点,具体怎么连通呢?以图中任一点为父节点,遍历其子节点(或者说是邻居结点),建立其任意两个子节点之间的联系,即(child1, child2)= (child1, father) * (father, child2),相当于以父节点为中转,建立第一结点与第三结点之间的联系。这样我们遍历完图中所有结点,就已经将图中有关联的结点互相关联了起来,其它的结点有可能并不联通,也就不会有关联了(构成的图可能是几个互不连通的子图)
因此我们在后续判断被除数和除数是否在图中时一定要判断是否在同一个图中,而不是说在整个大图中就好了。
class Solution {
public:
unordered_map<string, unordered_map<string, double>> map;
vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
// 构造双向带权图
for (int i = 0; i < equations.size(); i++) {
string from = equations[i][0], to = equations[i][1];
map[from][to] = values[i];
map[to][from] = 1.0 / values[i];
}
// 连接所有能连通的结点(打表)
for (auto &father : map) {
for (auto &child1 : map[father.first]) {
for (auto &child2 : map[father.first]) {
map[child1.first][child2.first] = map[child1.first][father.first] * map[father.first][child2.first];
}
}
}
vector<double> ret;
for (auto &query : queries) {
string from = query[0], to = query[1];
if (map.find(from) != map.end() && map[from].find(to) != map[from].end()) {
ret.push_back(map[from][to]);
} else {
ret.push_back(-1.0);
}
}
return ret;
}
};
解法三:并查集
精力有限,未深入研究。一篇介绍得很生动的并查集的文章:超有爱的并查集~。
struct Node {
double value;
Node* parent;
Node() : parent(this) {}
Node(double v) : value(v), parent(this) {}
};
class Solution {
unordered_map<string, Node*> m;
Node* find(Node* n) {
if (n->parent != n) {
n->parent = find(n->parent);
}
return n->parent;
}
void merge(Node* n1, Node* n2, double val) {
Node* p1 = find(n1);
Node* p2 = find(n2);
double ratio = n2->value * val / n1->value;
for (auto it : m) {
if (find(it.second) == p1) {
it.second->value *= ratio;
}
}
p1->parent = p2;
}
public:
vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
for (int i = 0; i < equations.size(); ++i) {
string a = equations[i][0];
string b = equations[i][1];
if (m.find(a) == m.end()) m[a] = new Node(values[i]);
if (m.find(b) == m.end()) m[b] = new Node(1.0);
merge(m[a], m[b], values[i]);
}
vector<double> res;
for (auto q : queries) {
if (m.find(q[0]) == m.end() || m.find(q[1]) == m.end() || find(m[q[0]]) != find(m[q[1]])) {
res.push_back(-1);
} else {
res.push_back(m[q[0]]->value / m[q[1]]->value);
}
}
return res;
}
};
题目七:Redundant Connection
题目描述
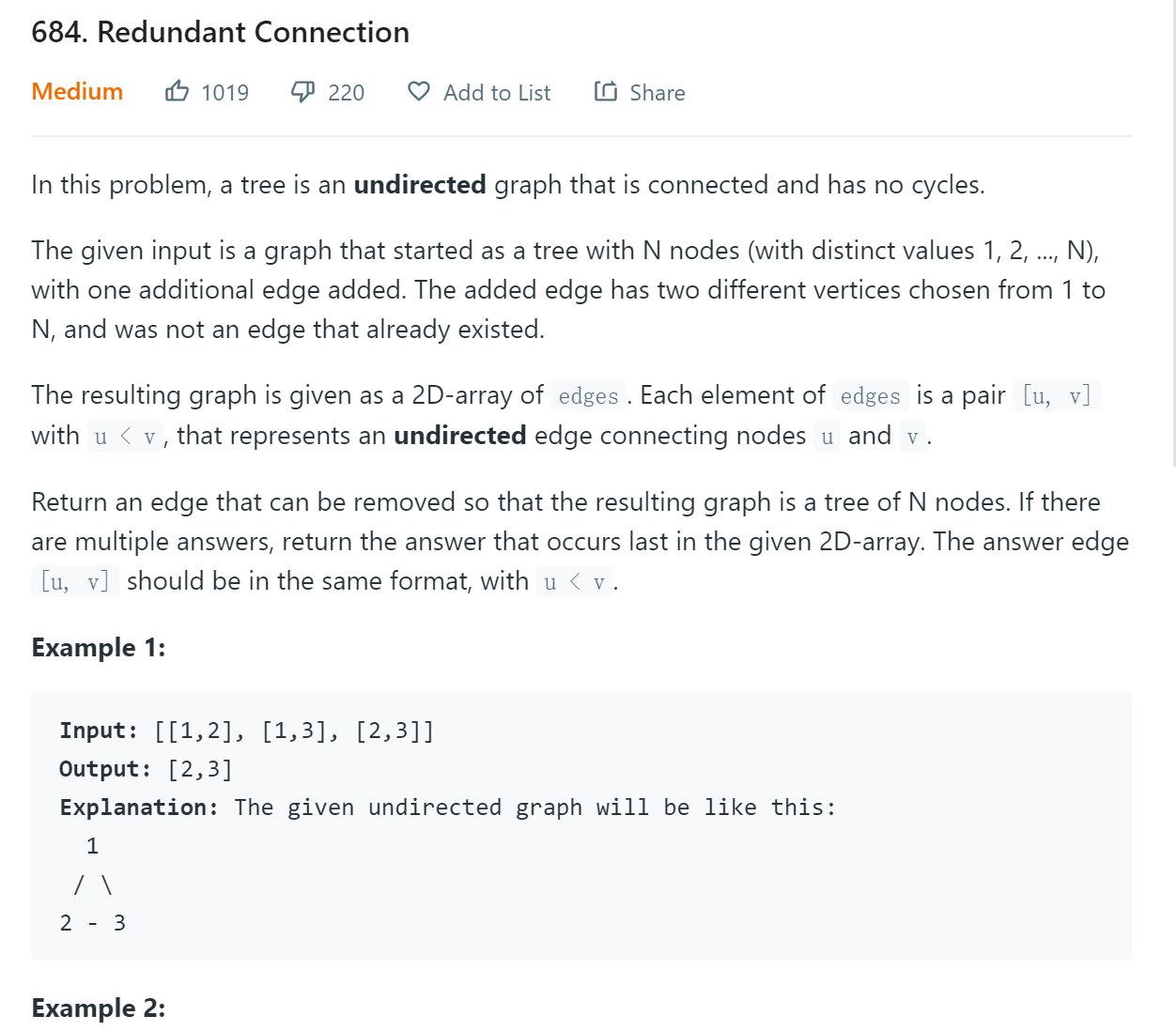
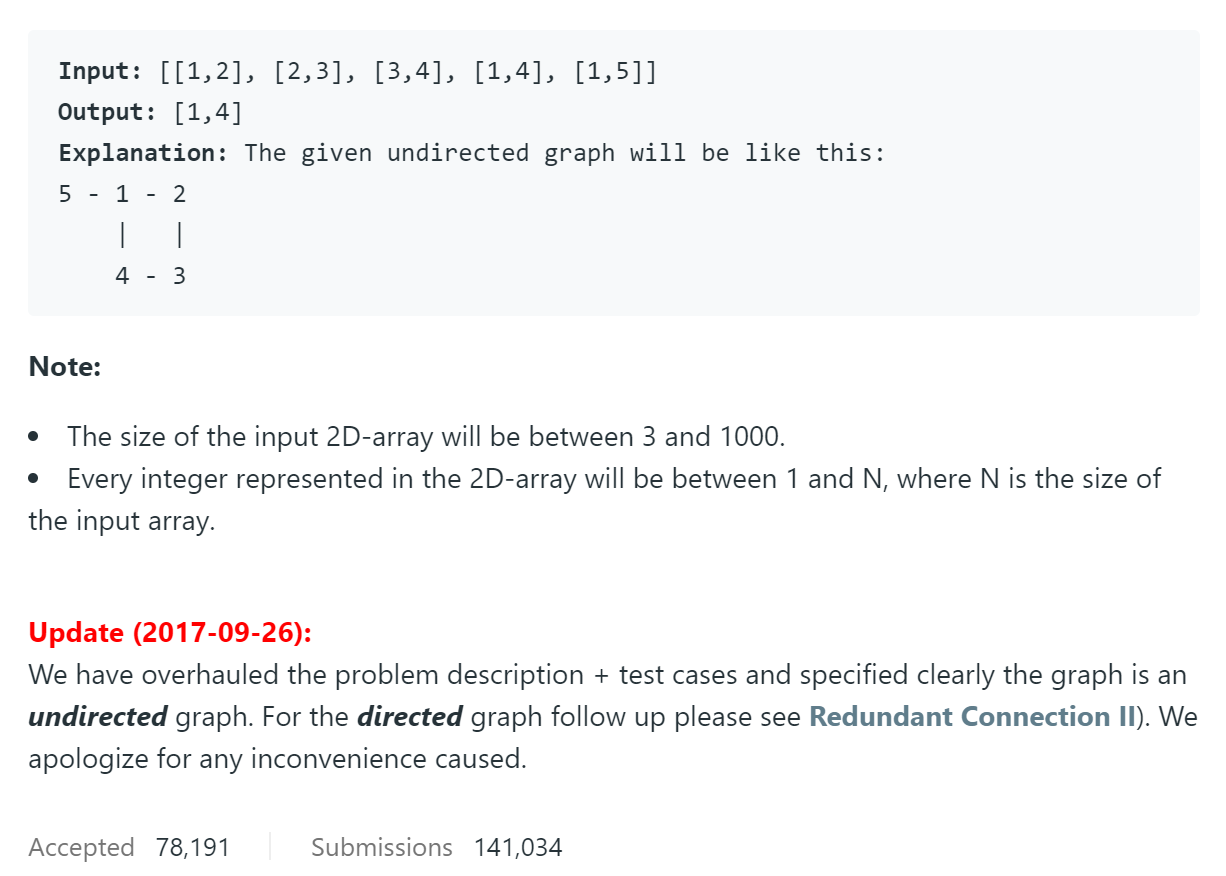
题目给出一组无向图的边,要求我们返回图中构成环的最后的一条边。
我的解法
DFS
采用邻接链表先构造好无向图,然后对给出的每一条边调用DFS深度优先遍历无向图,如果刚好该边能构成环,那么就直接返回(从后往前遍历,因此第一次遇到的就是构成环的最后一条边)。
我们需要构造一个visited数组来标识图中的结点是否遍历过,同时我们还需要一个pre结点来表示上一个结点,因为递归函数不可能知道上一层函数的内容,因此我们使用参数传递。这是防止遍历出现回溯,如:1-2,1的邻居有2,我们从1进入2,2的邻居有1,此时我们不能从2进入1,因为这样会导致死循环,而我们单纯的DFS又不知道我们就是从1来的,因此我们要添加一个变量pre来表示上一个结点1,这样我们就会在2的邻居里排除1,从而避免了回溯。
class Solution {
public:
unordered_map<int, vector<int>> map;
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
for (auto &edge : edges) {
map[edge[0]].push_back(edge[1]);
map[edge[1]].push_back(edge[0]);
}
vector<bool> visited(n+1, false);
for (int i = n-1; i >= 0; i--) {
if (isCircle(visited, edges[i][0], edges[i][0], edges[i][1])) {
return edges[i];
}
}
return {};
}
bool isCircle(vector<bool> &visited, int s, int pre, int e) {
if (!visited[e]) { //未遍历
if (s == e) { //成环
return true;
}
visited[e] = true; //遍历
for (int child : map[e]) {
if (child == pre) { // 回溯了,跳过
continue;
}
if (isCircle(visited, s, e, child) == true) {
return true;
}
}
visited[e] = false;
}
return false;
}
};
他人解法
解法一:优秀版DFS
图使用邻接链表实现,一开始为空,将每一条边按题目中给出的边的顺序一条条地加入图,如果加入一条边后图中刚好构成环,那么这条边就是构成环的最后一条边,也是我们要返回的边。
图的邻居我们使用unordered_set表示,在递归函数中,我们还需要添加参数pre,作用同上面的解法一样,不同的是该算法判断是否构成环特别简单,就是判断边的两个顶点s和e是否在一个连通图中,如果在的话就说明s能够到达e,此时外界再添加一条边(s,e),那么肯定就构成了环,而添加的这条边就是我们要的边。
而判断s和e是否在一个连通图中我们就调用DFS递归函数,递归判断s的邻居结点与e是否是邻居。
class Solution {
public:
unordered_map<int, unordered_set<int>> map;
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
for (auto &edge : edges) {
//构成环,直接返回
if (hasCircle(edge[0], edge[1], -1)) return edge;
map[edge[0]].insert(edge[1]);
map[edge[1]].insert(edge[0]);
}
return {};
}
bool hasCircle(int s, int e, int pre) {
//结点e是结点s的邻居,加上边(s,e)就构成了环
if (map[s].count(e)) return true;
for (auto &child : map[s]) {
if (child == pre) continue;
if (hasCircle(child, e, s)) return true;
}
return false;
}
};
解法二:并查集
相比于我上面的垃圾DFS,并查集算法实现起来是如此的优雅!相比于解法一,其实两者都是每次加入一条边,判断边的两个结点是否在同一个连通子图中,如果是的话就会构成环。但不同的是解法一使用图的数据结构,每次需要从一个起点s遍历所有邻居结点直到遇到e,这样才能判断边(s,e)的两个顶点是在同一个连通子图中,整个遍历是自上而下的,导致有很多冗余遍历,而并查集则是自下而上。
首先并查集不用图实现,而是构造一棵棵树(或者说是规定每个连通子图有一个根结点),每次要判断边(s,e)是否在同一个连通子图中,我们只需要判断顶点s和e是否在同一棵树上,而判断是否在同一棵树只需要知道双方的根结点是否是同一个结点就好了。于是我们定义了一个查找根结点的函数findRoot().
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
vector<int> root(n+1, -1);
for (auto &edge : edges) {
int root1 = findRoot(root, edge[0]);
int root2 = findRoot(root, edge[1]);
if (root1 == root2) {
return edge;
} else { //将两个连通子图连接起来
root[root1] = root2;
}
}
return {};
}
int findRoot(vector<int> &root, int v) {
while (root[v] != -1) {
v = root[v];
}
return v;
}
};
解法三:迭代版
罕见的迭代代码少于递归代码。思路是基于解法一的,但是运行时间远高于解法一。
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
unordered_map<int, unordered_set<int> > mp;
for (auto a : edges) {
queue<int> q{ {a[0]} };
unordered_set<int> s;
while (!q.empty()) {
int t = q.front(); q.pop();
if (mp[t].count(a[1]) != 0) return a; //a[1]是t的邻居(连通)
for (int num : mp[t]) {
if (s.count(num)) continue; //set存储遍历过的结点,避免回溯
q.push(num); s.insert(num);
}
}
mp[a[0]].insert(a[1]);
mp[a[1]].insert(a[0]);
}
return {};
}
};
题目八:Redundant Connection II
题目描述
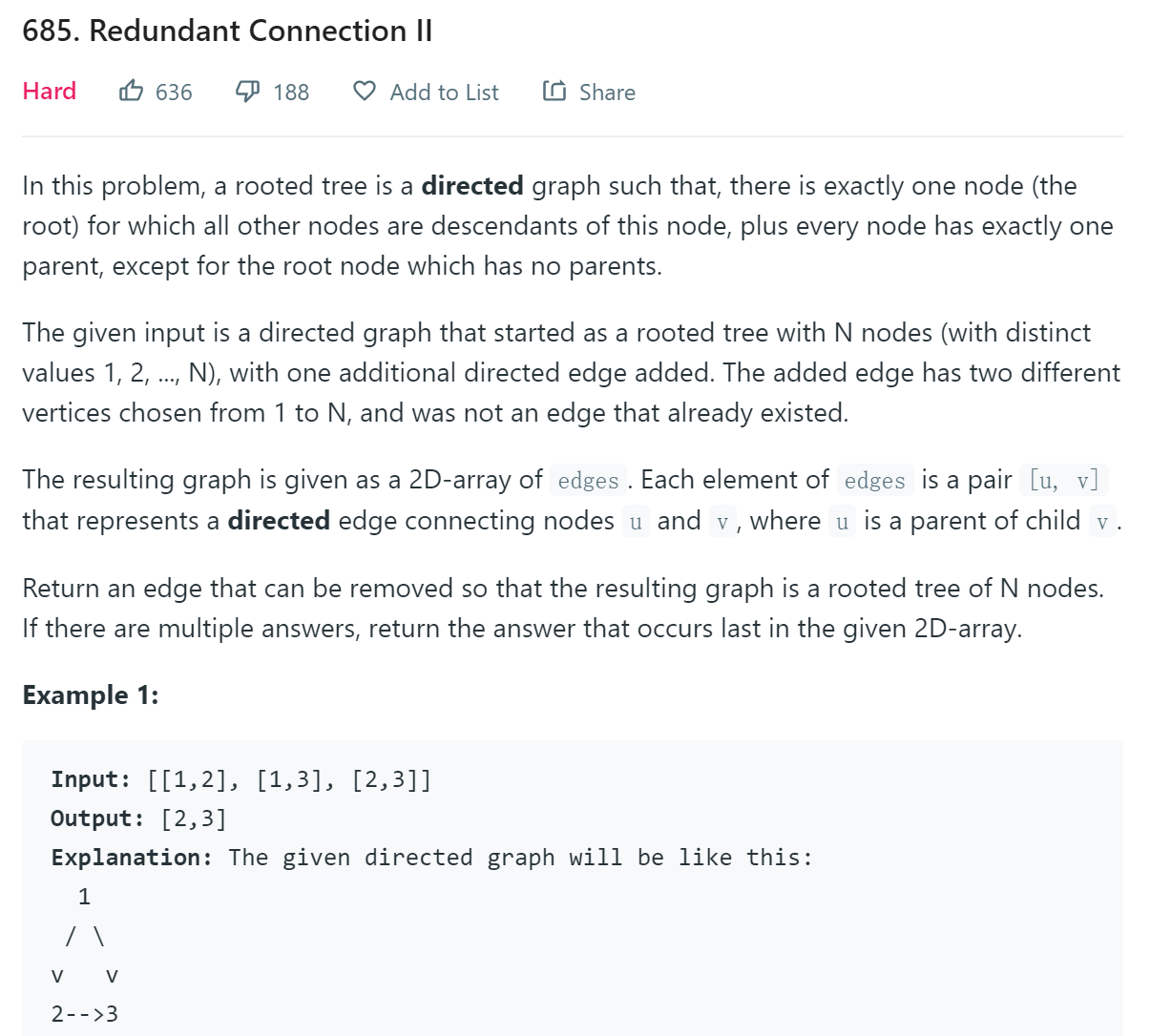
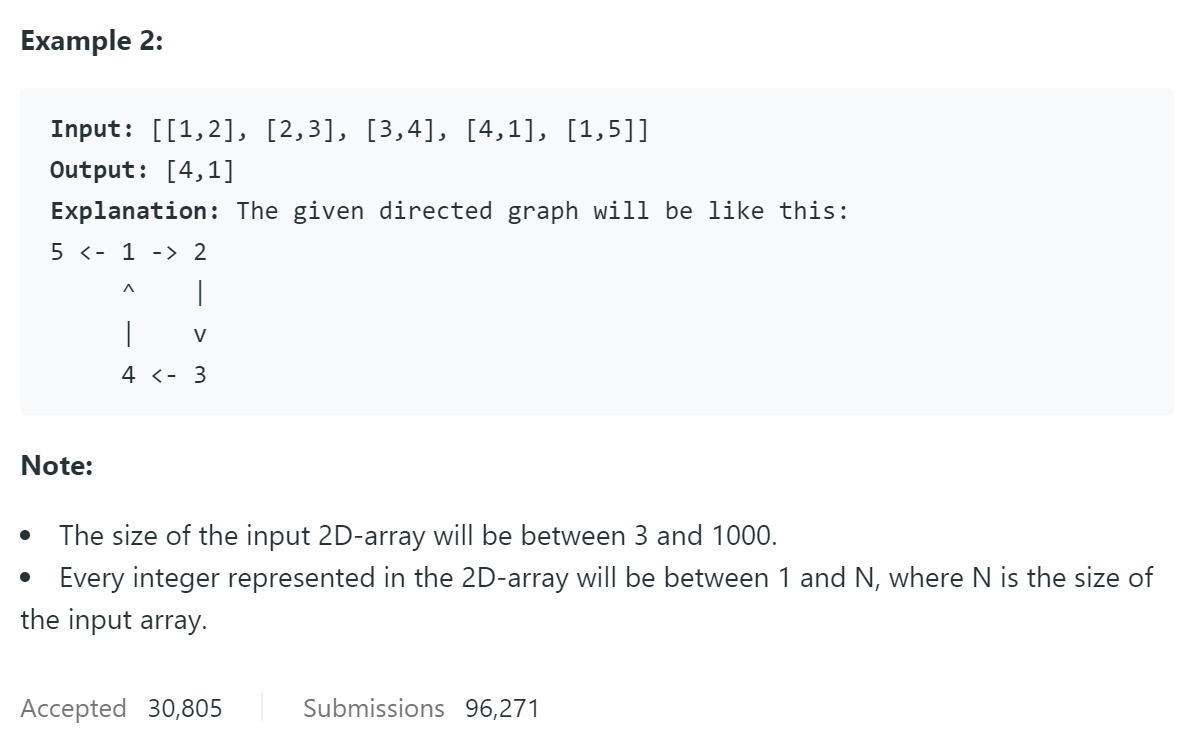
题目由上一题的无向图改为了有向图,其它条件大体不变,现在要我们删除一条有向边,使得剩余的图是一棵有根树。该树满足以下条件:
- 只有一个根节点
- 所有其他节点都是该根节点的后继
- 每一个节点只有一个父节点,除了根节点没有父节点。
我的解法
他人解法
解法一:并查集
由于每个结点只有一个父节点,每个结点的标号为1~n,且没有重复的边,因此一颗有根树有n个结点,那么就有n-1条边。现在有一条冗余的边,因此结点数就等于给出的边的数量。
冗余的边只有三种情况:
-
无环,但是有结点入度为2的结点(结点4)
[[1,2], [2,3], [3,4], [1,4]] 1 -> 2 | | v v 4 <- 3 -
有环,没有入度为2的结点
[[1,2], [2,3], [3,4], [4,1], [1,5]] 5 <- 1 -> 2 ^ | | v 4 <- 3 -
有环,且有入度为2的结点(结点1)
[[1,2], [2,3], [3,4], [4,1], [5,1]] 5 -> 1 -> 2 ^ | | v 4 <- 3因此我们首先遍历一遍看看是否有入度为2的结点,如果存在,那么保存该结点的两条边,同时删除其中一条边。然后我们测试剩下的边能不能组成环,这里我们用并查集实现。
- 如果剩下的边组成了环,并且存在入度为2的结点,那么说明我们删除错了,返回正确的那条边(情况3);
- 如果剩下的边组成了环但是没有入度为2的结点,那么就是普通的找环,返回组成环的最后一条边(情况2);
- 如果最终没有组成环,那么一定是存在入度为2的结点,并且我们删除的边恰好是冗余的边,返回我们删除的那条边(情况1)。
class Solution {
public:
vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
int n = edges.size();
vector<int> parent(n+1, 0), edge1, edge2;
//find if a node has 2 parents
for (auto &edge : edges) {
if (parent[edge[1]] != 0) {
edge1 = {parent[edge[1]], edge[1]}; //the first edge
edge2 = edge; // the second edge
edge[1] = 0; //set the second edge's child = 0, we just test the first edge
} else {
parent[edge[1]] = edge[0];
}
}
for (int i = 0; i <= n; i++) {
parent[i] = i;
}
for (auto &edge : edges) {
int father = edge[0], child = edge[1];
if (child == 0) continue;
if (findRoot(parent, father) == child) {//the first edge built a circle
if (edge1.size()) {
return edge1;
} else {
return edge;
}
}
parent[child] = father;
}
return edge2;
}
int findRoot(vector<int> &parent, int cur) {
while (parent[cur] != cur) {
parent[cur] = parent[parent[cur]];
cur = parent[cur];
}
return cur;
}
};
题目九:Network Delay Time
题目描述
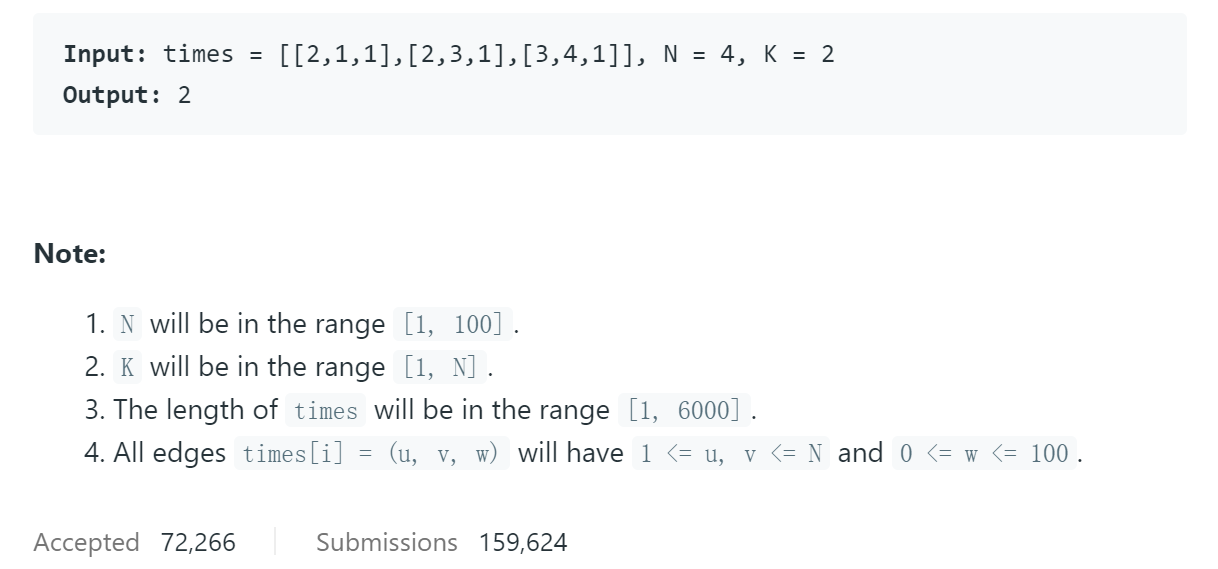
题目给出一个带权有向图,和一个起点k,要求k遍历所有结点得到的最大权值,如不能遍历所有结点返回-1.
我的解法
错误示范
搞了好久才搞出来一个递归,结果提交了才知道题目要求的是至少需要多久才能使所有结点收到信号,而我理解的是至多需要多久才能使所有结点收到信号,然后我就一个劲的深度递归遍历,试图找到权值最大的一条路。
node1 (N=3, K=1, node1->node3,node1->node2,weight = 2)
/ \
1 2
/ \
v v
node2 -2-> node3
[[1,2,1],[2,3,2],[1,3,2]]
3
1
其实题目问的是最短路径,例如上例,我给出的答案是node1->node2->node3,权值为3,而实际上node1到node3的最短距离为2。
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
vector<bool> visited(N+1, false);
unordered_map<int, unordered_map<int, int>> graph;
for (auto &time : times) {
int u = time[0], v = time[1], w = time[2];
graph[u][v] = w;
}
int maxTime = 0;
DFS(graph, K, maxTime, 0, visited, N);
return N > 0 ? -1 : maxTime;
}
void DFS(unordered_map<int, unordered_map<int, int>> &graph, int k, int &maxTime, int sum, vector<bool> &visited, int &nodes) {
nodes--;
if (graph[k].empty()) {
maxTime = max(maxTime, sum);
return;
}
if (visited[k] == true) {
nodes++;
return;
}
maxTime = max(maxTime, sum);
visited[k] = true;
unordered_map<int, int>::iterator iter;
for (iter = graph[k].begin(); iter != graph[k].end(); iter++) {
DFS(graph, iter->first, maxTime, sum+iter->second, visited, nodes);
}
visited[k] = false;
}
};
他人解法
解法一:Dijkstra算法
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
const int inf = 1000;
vector<vector<int>> dist(N+1, vector<int>(N+1, inf));
vector<bool> visited(N+1, false);
//建立邻接矩阵
for (auto &time : times) {
int u = time[0], v = time[1], w = time[2];
dist[u][v] = w;
}
dist[K][K] = 0;
for (int i = 0; i < N; i++) {//确定N-1条最短路径
//在未确定最短路径的结点中找距离起点最近的结点
int mini = inf, minindex = 0;
for (int j = 1; j <= N; j++) {
if (!visited[j] && dist[K][j] < mini) {
mini = dist[K][j];
minindex = j;
}
}
visited[minindex] = true;//找到后就确定了其最短路径
for (int j = 1; j <= N; j++) { //用刚刚确定的结点做松弛操作
if (!visited[j] && j != minindex && dist[K][j] > dist[K][minindex]+dist[minindex][j]) {
dist[K][j] = dist[K][minindex] + dist[minindex][j];
}
}
}
int maxp = 0;
for (int i = 1; i <= N; i++) {
maxp = max(maxp, dist[K][i]);
}
return maxp==inf ? -1 : maxp;
}
};
解法二:Bellman-Ford算法
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
const int inf = 1000;
vector<vector<int>> dist(N+1, vector<int>(N+1, inf));
for (auto &time : times) {
dist[time[0]][time[1]] = time[2];
}
dist[K][K] = 0;
for (int i = 0; i < N; i++) {//N-1次松弛所有边
for (auto &edge : times) {
int u = edge[0], v = edge[1], w = edge[2];
if (dist[K][v] > dist[K][u] + w) {
dist[K][v] = dist[K][u] + w;
}
}
}
int maxp = *max_element(dist[K].begin()+1, dist[K].end());
return maxp == inf ? -1 : maxp;
}
};
解法三:floyd算法
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
const int inf = 1000;
vector<vector<int>> dist(N+1, vector<int>(N+1, inf));
for (auto &time : times) {
dist[time[0]][time[1]] = time[2];
}
for (int k = 1; k <= N; k++) {//以k为中点松弛所有边
dist[k][k] = 0;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
if (dist[i][k]+dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
int maxp = *max_element(dist[K].begin()+1, dist[K].end());
return maxp == inf ? -1 : maxp;
}
};
解法四:SPFA算法
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
const int inf = 1000;
vector<vector<pair<int,int>>> dist(N+1);
vector<bool> inQue(N+1, false);
vector<int> d(N+1, inf);
for (auto &time : times) {
int u = time[0], v = time[1], w = time[2];
dist[u].push_back({v, w});
}
d[K] = 0;
queue<int> que;
while (!que.empty()) {
int u = que.front(); que.pop();
inQue[u] = false;
for (auto &v_w : dist[u]) {
if (d[v_w.first] > d[u] + v_w.second) {
d[v_w.first] = d[u] + v_w.second;
if (!inQue[v_w.first]) {
que.push(v_w.first);
inQue[v_w.first] = true;
}
}
}
}
int maxp = *max_element(d.begin()+1, d.end());
return maxp == inf ? -1 : maxp;
}
};
题目十:Couples Holding Hands
题目描述
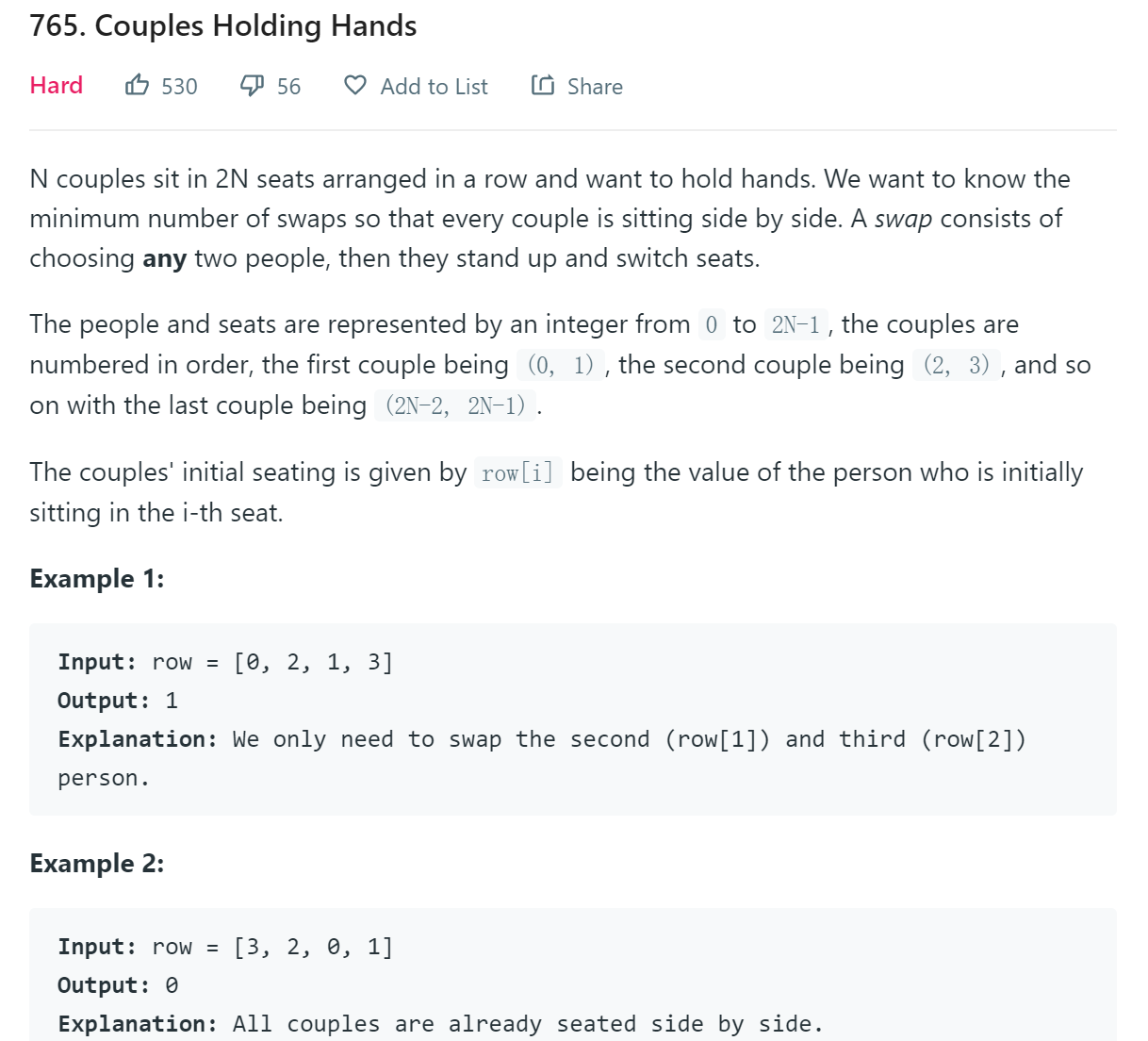
题目给出n对情侣以及n张情侣座位,一张情侣座位能坐下一对情侣,情侣座位呈一排排列。现在n对情侣打乱随意分配给n张情侣座,要使得情侣座上的都是情侣,至少要交换几次座位。题目给出一个由0开始的连续自然数组成的乱序数组来表示打乱座位的情侣,其中(0, 1)、(2, 3)、(4, 5)……分别都表示一对情侣。
我的解法
并查集
根据题目的提示,将分散开的情侣双方所在的座位作为结点连接起来组成无向图。根据规律,最少的交换次数和图中结点数(或者边数)以及连通图的数量有关。但是我还是没搞清楚具体的关系。
第二天,在看了一丢丢别人的题解的前提下,我还是理出了思绪,其实只要算出无向图中的连通图数量和图中的结点数量,那么最少的交换次数就是结点数减去连通图的数量。怎么证明呢?
如果一开始所有的情侣都已经和对象坐在了一起,那么就会有n个连通分量,即n个结点互不连接,我们要的就是这个状态。如果有对象乱坐,假设此时有k个连通分量,而此时我们交换一次最多就增加一个单独结点的连通分量(将其从一大坨结点组成的连通分量中扯下来)。那么问题来了:总共n个结点组成了k个连通分量,每次交换座位增加一个连通分量,交换几次才有n个连通分量呢?答案:n-k
这里的n很好算就是人头数除以2,而k比较难算,我是使用并查集计算,每个两桶分量有一个代表,判断两个结点是否属于一个连通分量时,只需要判断其所在连通分量的代表是否是同一个结点即可。
class Solution {
public:
int minSwapsCouples(vector<int>& row) {
int n = row.size() / 2;//there are n seats
vector<vector<int>> graph(n, vector<int>());
for (int i = 0; i < row.size(); i++) {
int seat = i / 2, couple = row[i] / 2;
graph[couple].push_back(seat);//couple=i means i,i+1;seat=i means index i,i+1
}
vector<int> parent(n, -1);
for (auto &seats : graph) {
int root1 = findRoot(parent, seats[0]);
int root2 = findRoot(parent, seats[1]);
if (root1 != root2) {
parent[root2] = root1;
}
}
set<int> circles;
for (int i = 0; i < n; i++) {//find the number of circles
int root = findRoot(parent, i);
circles.insert(root);
}
return n - circles.size();
}
int findRoot(vector<int> &parent, int cur) {
while (parent[cur] != -1) {
cur = parent[cur];
}
return cur;
}
};
他人解法
解法一:并查集
与上面的并查集不同,这里我们建立连通分量的结点不是座位序号,而是情侣序号,把坐在同一张情侣座上的两个人所在的情侣序号作为结点连接起来。如果坐在一起的本身就是一对情侣,那么我们就不做任何操作,该情侣序号独自作为一个连通分量。如果坐在一起的两个人不是情侣,那么首先检查两个人的情侣序号是否在一个连通分量中,如果在一个连通分量的话就不做任何操作,否则就合并两个连通分量,并将连通分量总数(连通分量总数)减一。
而最少的交换次数就是总的结点数(情侣对数)- 连通分量数(解释同上)。
class Solution {
public:
int minSwapsCouples(vector<int>& row) {
int n = row.size(), circles = n / 2;
vector<int> root(n, -1);
for (int i = 0; i < n; i += 2) {
int root1 = find(root, row[i] / 2);
int root2 = find(root, row[i + 1] / 2);
if (root1 != root2) {
root[root1] = root2;
--circles;
}
}
return n / 2 - circles;
}
int find(vector<int>& root, int i) {
return (root[i] == -1 ? i : find(root, root[i]));
}
};
解法二:贪心算法
直接从零号座位开始遍历所有座位,以座位上的第一个人为基础,如果第二个人不是其对象,那么将第二个人与第一个人的对象交换座位。这样我们只需要遍历前n-1个座位,即把前面的座位都调整好了,那么最后一个座位上的一定是情侣。这种交换的方式一定是交换次数最少的,因为每次交换都至少有一对情侣成功地坐在一起。如果有那么几组情侣只要交换一次就可以让两对情侣成功坐在一起,那么我们使用贪心算法处理当前座位时,我们的交换操作同样也会让两对情侣坐在一起。
下面的代码使用异或可以快速得到一个人的同伴,例如3的同伴是2而不是4,3^1=2。注意:交换了row中的位置后记得还要交换他们在pos中的位置。
class Solution {
public:
int minSwapsCouples(vector<int>& row) {
int n = row.size(), swaps = 0;
vector<int> pos(n);
for (int i = 0; i < n; i++) {
pos[row[i]] = i; //store the position of row[i] in array row
}
for (int i = 0; i < n; i += 2) {
int partner = row[i] ^ 1, near = row[i+1];
if (near != partner) { //the near one is not partner
swap(row[pos[near]], row[pos[partner]]); //swap them in row
swap(pos[near], pos[partner]); //swap them in pos
swaps++;
}
}
return swaps;
}
};
我的leetcode之旅就先告一段落吧,为了更好地提高自己,我在接下来的时间里打算先把《剑指offer》的题目做完并总结吸收,后续再回归leetcode。到时候刷题应该不是以题目为单位做总结了,更可能是以知识点为单位做知识总结。
