图的表示？关联矩阵、邻接矩阵、邻接链表

zhyjc6于2020-03-11发布 约2061字·约4分钟 本文总阅读量次

图的定义

简单图、多重图、有向图、无向图，这些都是图（这里先不一一介绍了），但我们通常使用以下两种方式统一定义：

二元组的定义

一张图 $G$是一个二元组 $(V,E)$，其中$V$称为顶点集（Vertices set），$E$称为边集（Edges set）。它们亦可写成$V(G)$和$E(G)$。$E$的元素是一个二元组数对，用$(x,y)$表示，其中$x,y \in V$。

三元组的定义

一张图 $G$ 是一个三元组 $(V,E,I)$，其中$V$称为顶集（Vertices set），$E$称为边集（Edges set），$E$与$V$不相交；$I$称为关联函数，$I$将$E$中的每一个元素映射到$V \times V$。如果 $I(e)=(u,v)(e\in E,u,v\in V)$，那么称边$e$连接顶点$u,v$，而$u,v$则称作$e$的端点，$u,v$ 此时关于$e$ 相邻。同时，若两条边$i,j$ 有一个公共顶点$u$ ，则称$i,j$ 关于$u$ 相邻。

图的存储表示

邻接矩阵表示

邻接矩阵（adjacency matrix）是表示顶点之间相邻关系的二维数组。

我们通常会将图 $G$ 中的结点编为1，2，…，|$V$| （这种编号可以是任意的），然后使用一个 |$V$| $ \times $|$V$| 的矩阵 $A=(a_{ij})$ 表示，该矩阵满足以下条件：

\[a_{ij}=\begin{cases} 1 &若(i,j)\in E\\ 0 &其它\\ \end{cases}\]

现在我们来看看邻接矩阵在分别在无向图中和有向图中的表示吧：

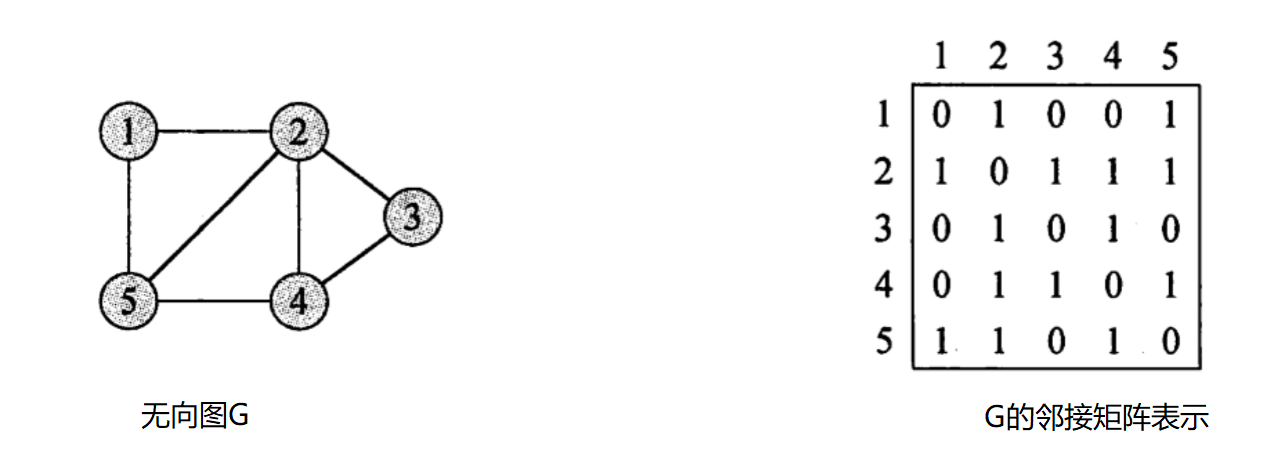
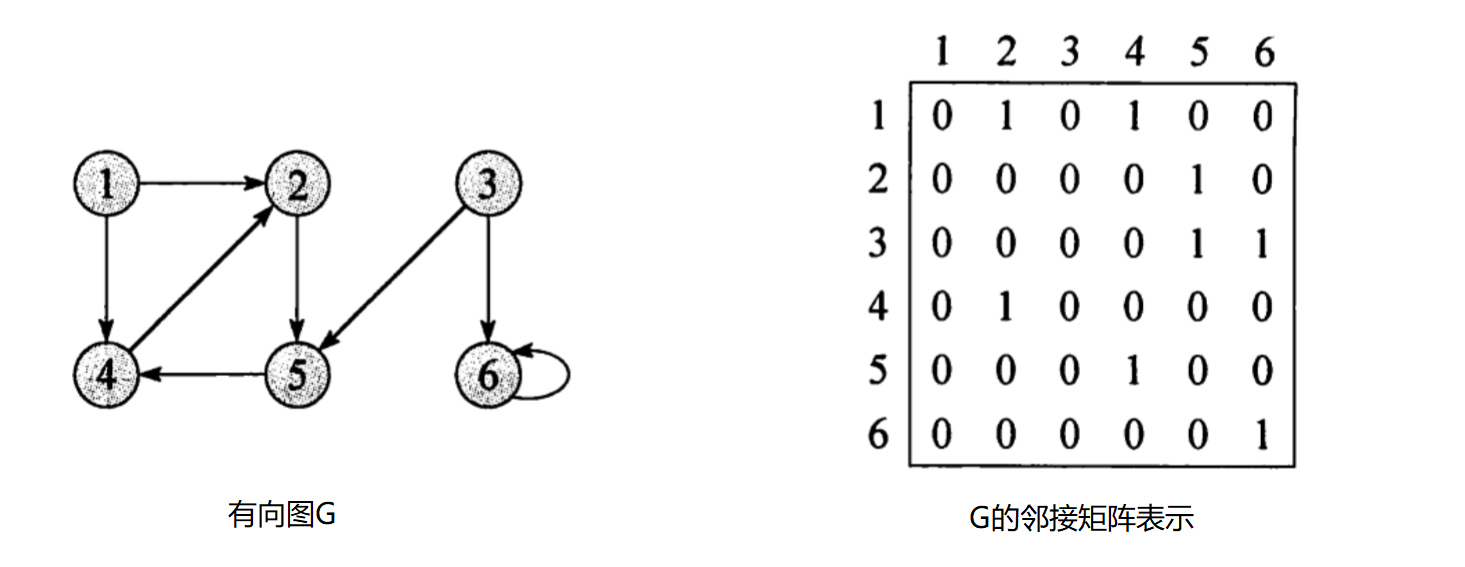
可以看出邻接矩阵是在无向图的表示中是转置矩阵，而在有向图中则不是。

对于带权图来说，可以将$a_{ij}$ 用来存储权值，如果两结点无连接，用0或无穷表示：

\[a_{ij}=\begin{cases} w_{ij} & 若(i,j) \in E\\ 0或\infty & 其它\\ \end{cases}\]

特点

邻接链表表示

邻接链表（adjacency list）由图中的每一个结点及其相邻结点生成以该结点为头结点的一组链表。

当处理稀疏图时，相对于邻接矩阵，邻接链表无需一次就分配那么大的空间，而是在遍历图的过程中一点一点地分配，它是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点，则把相邻顶点依次存放于表头结点所指向的单向链表中。

虽然邻接链表是一种非常节约空间的结构，但在无向图中用邻接链表表示也会出现数据冗余。这是因为表头结点A所指链表中存在一个指向C的表结点的同时，表头结点C所指链表也会存在一个指向A的表结点。

现在我们来看看无向图和有向图中的邻接链表是怎么表示的吧：

无向图

有向图

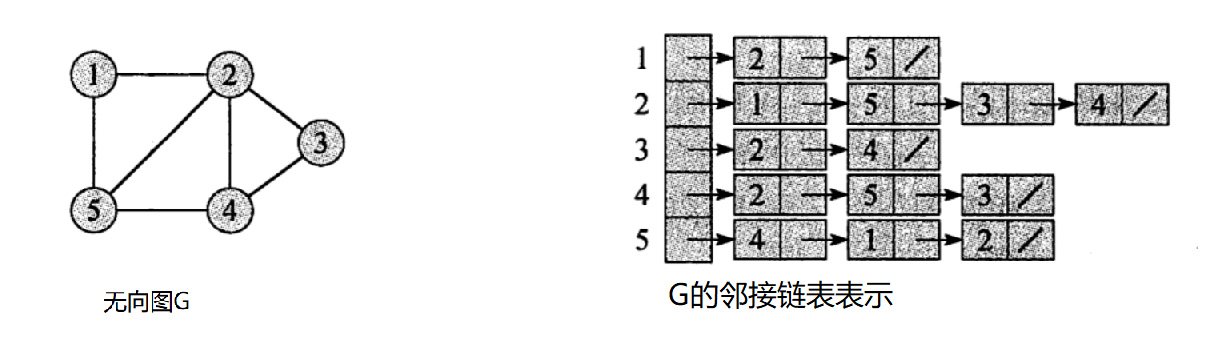
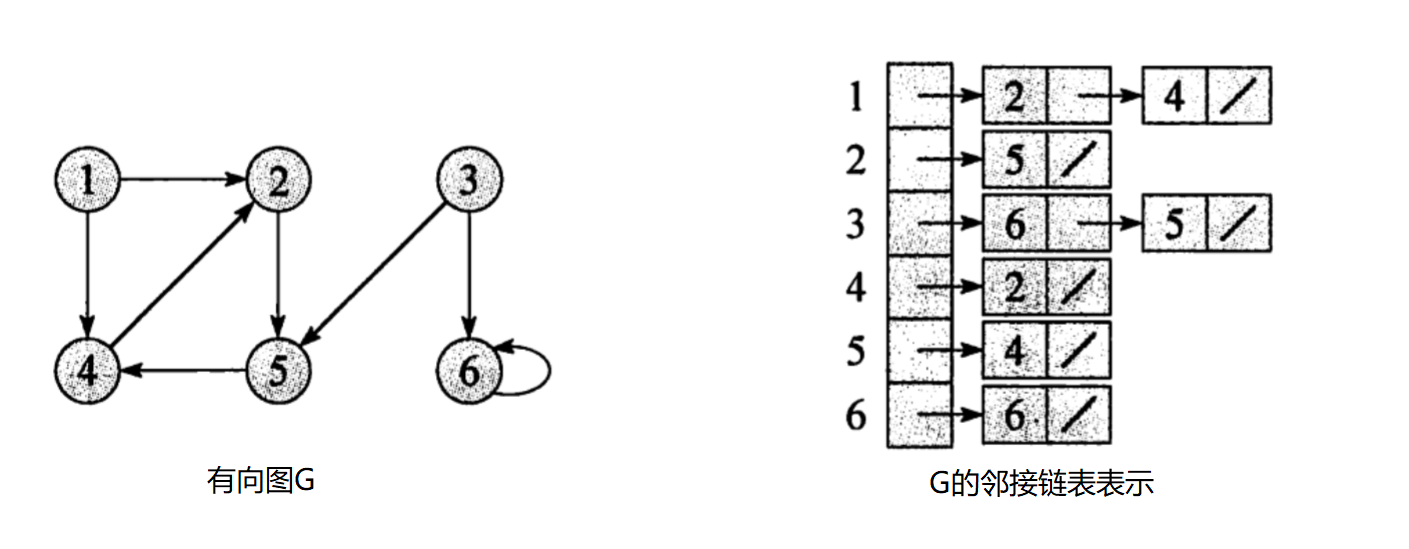
特点

关联矩阵表示

邻接矩阵和邻接链表都是用来表示图中各个点和每个点之间的关系，而关联矩阵（incidence matrix）即用一个矩阵来表示各个点和每条边之间的关系。

定义

设无向图 $G=(V, E)$，其中顶点集 $V=v_1,v_2,⋯,v_n$, 边集 $E=e_1,e_2,⋯,e_m$，用 $a_{ij}$ 表示顶点$v_i$与边$e_j$ 关联的次数，可能取值为0, 1, 2, ….，我们称所得矩阵$A=A(G)=(a_{ij})_{n\times m}$为图 G 的关联矩阵

右图中的每一行代表左图中对应的的每一个结点，右图中的每一列代表左图中对应的每一条边。例如：

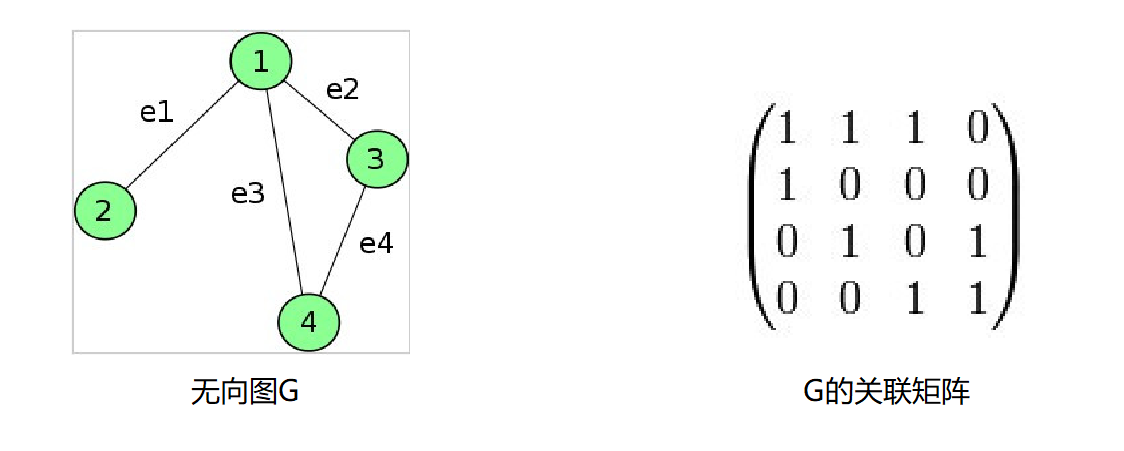
对于关联矩阵第一行1 1 1 0，表示点$v_1$和各边的关系。如图所示，$v_1$和$e_1,e_2,e_3$相连，和$e_4$未连，故关联矩阵的值为1 1 1 0. 下面各行为点$v_2，v_3, v_4$ 和各边的关联，以此类推。因此每一行值的总和为该点的度。

对于有向图，若$b_{ij}$ = 1，表示边j离开点i。 若 $b_{ij}$= -1， 表示边j进入点i。 若 $b_{ij}$ = 0，表示边j和点i不相关联。

复杂度比较

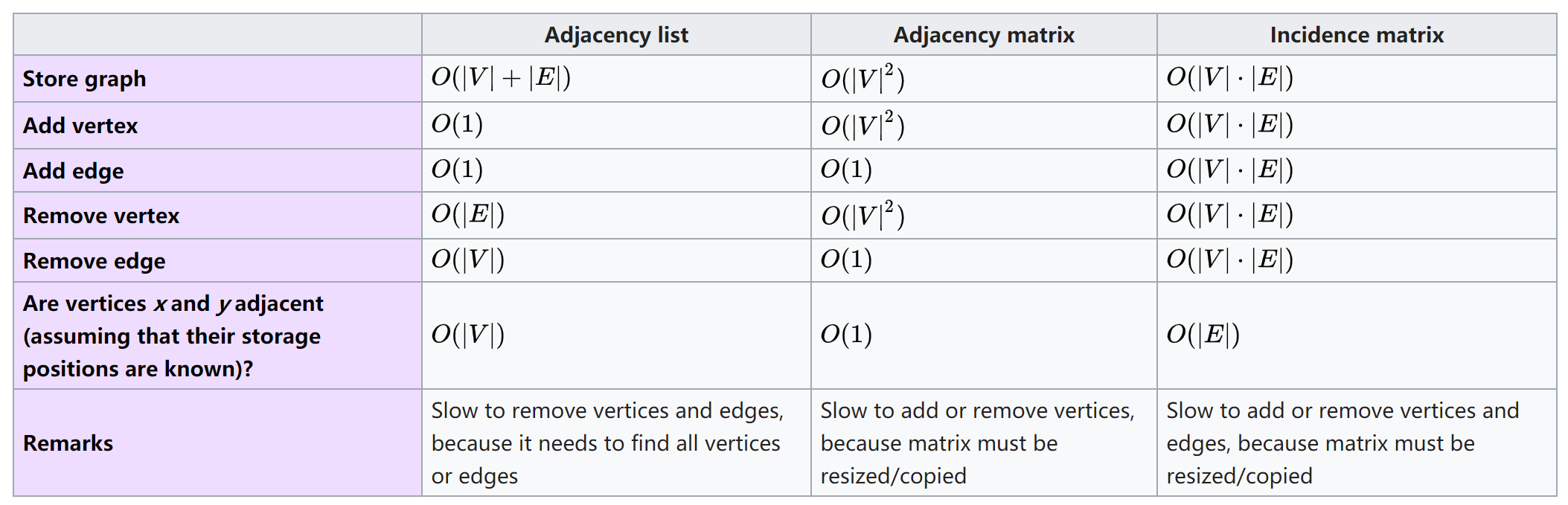
参考资料