我们熟知的快速排序以及堆排序的时间复杂度仅为$O(nlgn)$,还不是线性时间。那它们能不能突破这个界限达到线性时间复杂度呢?答案是不能,原因在于这类排序算法的本质是基于比较。而基于比较的排序算法理论上就有一个下界,该下界就是$O(nlgn)$,怎么理解呢?
决策树模型
比较排序可以被抽象为一颗决策树。决策树是一颗完全二叉树,它可以表示在给定输入规模的情况下,某一特定排序算法对所有元素的比较操作。但其中控制、数据移动等操作都被忽略了。
在决策树中,每个非叶子结点都以$i:j$标记,表示元素$i和j$作比较,其中$i$和$j$满足$1\le i,j \le n$,$n$ 是输入序列中的元素个数。左子树表示在确定了 $a_i \le a_j$之后的后续比较,右子树则表示在确定了 $a_i>a_j$之后的后续比较。每个叶子结点都表示比较后的结果之一。
例如输入序列($a_1,a_2,a_3$),其决策树如下
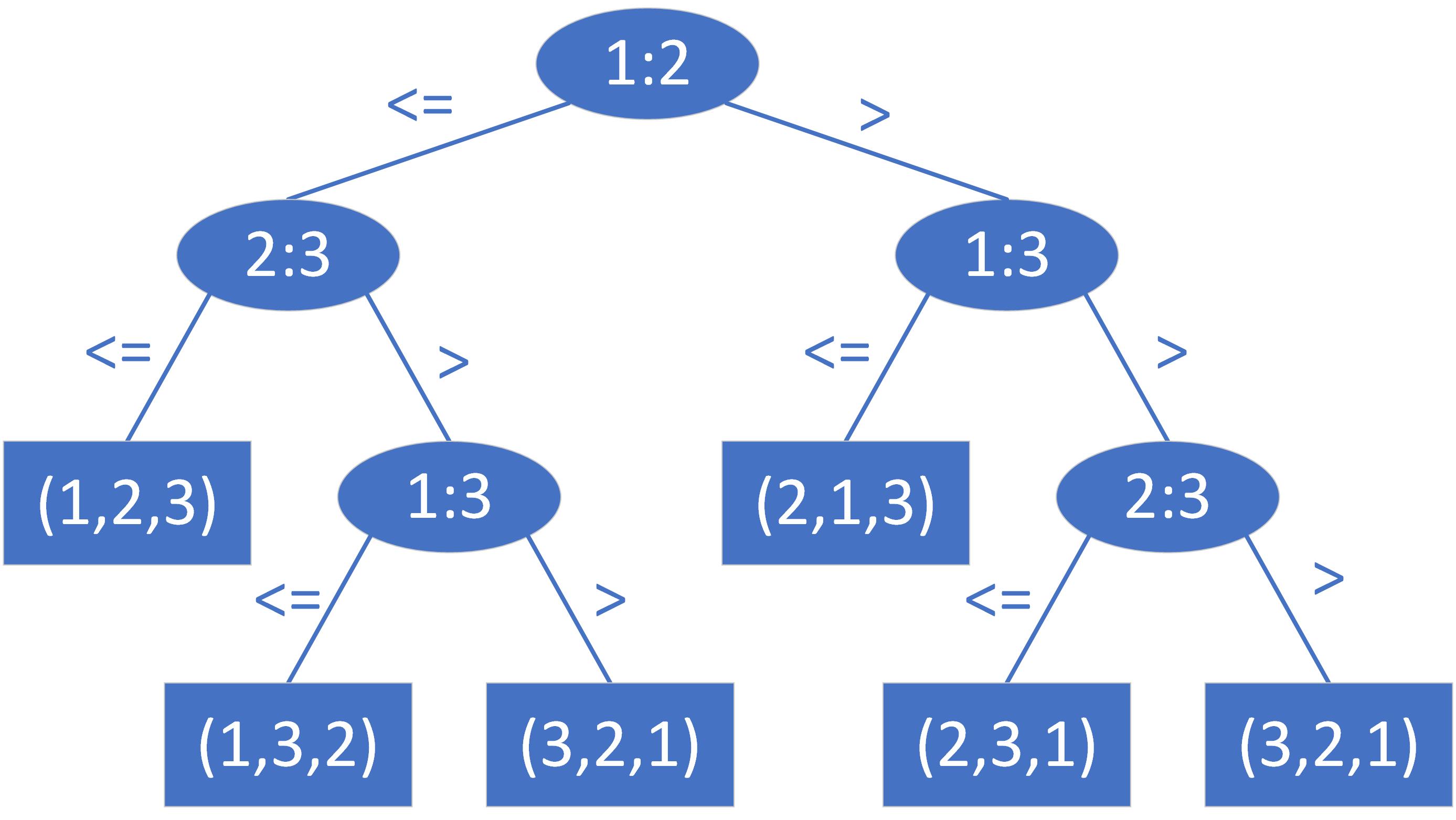
对于一个包含$n$个元素的输入来说,若元素互不相同,那么输入序列的可能情况有$n!$种。因为任何正确的排序算法都能够生成输入的每一个排列,所以对一个正确的比较排序算法而言,$n$个元素的$n!$种可能的排列都应该出现在决策树的叶子结点上。
在决策树中,从根结点到任意一个可达叶结点之间最长简单路径长度,表示的是对应排序算法中最坏情况下的比较次数(反之最短的那条路表示的是最好情况下的比较次数)。因此,一个比较排序算法中的最坏情况比较次数就等于其决策树的高度。同时,当决策树中每种排列都是以可达的叶节点的形式出现时该决策树的高度的下界也就是比较排序算法运行时间的下界。
定理:在最坏情况下,任何比较排序算法都需要做$\Omega(nlgn)$次比较
考虑一颗高度为$h$、具有$l$个可达叶结点的决策树,它对应一个对$n$个元素所做的比较排序。因为输入数据的$n!$种可能的排列都是叶结点,所以有
$n! \le l$
由于在一棵高度为$h$的二叉树中,叶结点的数目不多于$2^h$,我们可以得到
$n! \le l \le 2^h$
对该式两边取对数,有
$h \ge lg(n!) \Rightarrow h=\Omega(nlgn)$
阶乘函数的一个弱上界是$n! \le n^n$,因为在阶乘中,$n$项的每项最多为$n$;一个弱下界是$2^n$,因为除了$n=1或0$,在阶乘中,$n$项的每一项最少为$2$。但斯特林(Stirling)近似公式给出了一个更紧确的上界和下界:
$n!=\sqrt{2\pi n}(\frac{n}{e})^n(1+\Theta(\frac{1}{n}))$
从而得到:
$lg(n!)=\Theta(nlgn)$
由此可以推出堆排序和归并排序都是渐进最优的比较排序算法,因为它们逼近了比较排序算法的下界。
以上都是基于比较的排序算法,而接下来要介绍的三种线性时间复杂度算法都完全没有输入元素之间的比较,已经脱离了比较排序的模型,因此能够突破$\Omega(nlgn)$的下界。
计数排序
计数排序是稳定排序。假设$n$个输入元素中的每一个都是在$0$到$k$区间内的一个整数,当$k=O(n)$时,排序的运行时间为$\Theta(n)$
算法思想
对每一个输入元素$x$,确定小于$x$的元素个数。从而可以直接将其放在待输出数组中的正确位置。例如,如果有$13$个元素小于$x$,则$x$就应该在第$14$个输出位置上。当有元素相同时,我们的方案还需要改进。
伪代码
假设输入是一个数组A[1..n],A.length=n。我们还需要两个数组:B[1..n]存放排序后的输出,C[0..k]提供临时存储空间。
counting-sort(A,B,k)
let C[0..k] be a new array
for i = 0 to k
C[i] = 0
for j = 1 to A.length
C[A[j]] = C[A[j]] + 1
//C[i] now contains the number of elements equal to i.
for i = 1 to k
C[i] = C[i] + C[i-1]
//C[i] now contains the number of elements less or equal to i.
for j = A.length downto 1
B[C[A[j]]] = A[j]
C[A[j]] = C[A[j]] - 1
时间复杂度
第$3\sim4$行数组C初始化的for循环所花时间为$\Theta(k)$;第$5\sim 6$行计算每个元素出现次数的for循环所花时间为$\Theta(n)$;第$8\sim 9$行计算排在每个元素前面元素个数的for循环所花时间为$\Theta(k)$;第$11\sim 13$行for循环所花时间为$\Theta(n)$。因此总的时间为$\Theta(k)+\Theta(n)+\Theta(k)+\Theta(n)=\Theta(n+k)$
实际上我们一般只有在$k=O(n)$的时候才用计数排序,因为只有这样才能使$\Theta(n+k)=\Theta(n)$
空间复杂度
空间复杂度为$O(n+k)$。需要两个辅助数组:存放临时结果的C[k],存放排序结果的B[n]。
正是因为计数排序是稳定排序,所以基数排序中常常使用计数排序作为辅助排序算法。
基数排序
基数排序(radix sort)属于稳定排序,是一种用在卡片排序机上的算法,属于“分配式排序”(distribution sort),顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用。
算法思想
一般的排序只能将元素作为一个整体按其大小或某一种方式排序,而基数排序则是可以按照元素中各个部位的权重来进行定制化排序(我们可以自定义某一部分的权重)。
比如我们要排序一些三元组(a,b,c),要求按照a为首要关键字、b为第2关键字、c为第3关键字进行排序。
我们可以首先按照首要关键字排序,得到首要关键字相同的若干组,再分别对各组中按照第2关键字进行排序,每组再得到若干小组,然后再对这些小组按照第3关键字排序。每个小组都有序后,最后再将各个小组按照大组的顺序串联起来。这种基数排序我们称作MSD(Most Significant Digital)排序
如果我们使用稳定的排序,并且先按照第3关键字排序,再按照第2关键字排序,最后按照第1关键字排序,最终得到排序结果。这种基数排序我们称作LSD(Least Significant Digital)排序。这里注意我们必须使用稳定排序,否则较低权重排序结果可能会被较高排序结果打乱。
如果待排序的元素是一组数。那么我们可以按照从高位到低位权重逐渐降低的策略划分权重,因为在数的大小比较中,权重最大的自然是最高位,如果最高位都比不过,那么后面的低位就不用比了。为了节约空间以及实现方便,我们一般使用LSD排序方法,将一组数从低位到高位,依次按照每一位的大小来排序,直到最高位排序完毕(高位不足补0),此时得到的结果就是排序的结果。
伪代码
假设数组A中有n个d位的元素(高位不足补0),其中第1位是最低位,第d位是最高位。
radix-sort(A, d)
for i=1 to d
use a stable sort to sort array A on digit i
定理:给定n个d位数,其中每一个数位有k个可能的取值。如果radix-sort使用的稳定排序方法耗时为$\Theta(n+k)$,那么它就可以在$\Theta(d(n+k))$时间内将这些数排好序。
时间复杂度
给定n个d位数,其中每一个数位有k个可能的取值。如果我们选取计数排序作为每一位的稳定排序方法,那么每一位的耗时为$\Theta(n+k)$,因此总耗时就是$\Theta(d(n+k))$。当d为常数且$k=O(n)$时,总排序时间为$ \Theta(n)$
桶排序
算法思想
桶排序假设输入数据是均匀分布的,这样我们就可以将这些数据均匀分布到一定数量的大小相同的桶中,而不至于桶中数据的量相差太大。而由于桶之间已经是排好序的(我们构造一系列有序的桶),因此以桶为单位的大块数据之间也就是已经排好序的,我们只需要将每个桶中的数据进行排序,再将所有数据从每一个桶中依次取出来就完成了排序。
这里涉及到几个比较重要也是比较难的点:
- 桶的数据结构实现
- 桶的数量
- 桶中的排序算法
桶我们可以使用链表或者直接使用数组来进行实现,具体如何选择就看当时的需求以及我们对数据结构的熟练程度。桶的数量则是空间与时间的权衡,桶的数量越多,多到和输入数据一样多,这样每个桶中最多就1个元素(相同元素看作一个元素),那么就不需要桶中的排序算法了,但是这样牺牲了空间;桶的数量越少,少到只有一个桶,那就是全靠桶中的排序算法了,如果使用的是比较排序算法,那么时间复杂度就最多为$O(nlgn)$,节约了空间却牺牲了时间。桶中的排序算法多使用插入排序。
伪代码
下面的桶排序伪代码将[0, 1]区间划分为n个相同大小的子区间,也就是桶。因为输入是均匀、独立地分布在[0, 1)区间上,所以一般不会出现很多数落在一个桶中的情况。
当然我们在使用的过程中可以将[0, 1)区间扩展为任意区间。当然桶的数量也不一定就是n,可以根据需要更改为更合适的值。
bucket-sort(A)
n = A.length
let B[0..n-1] be a new array
for i = 0 to n-1
make B[i] an empty list
for i = 0 to n-1
insert A[i] into list B[$\lfloor nA[i]\rfloor$]
for i = 0 to n-1
sort list B[i] with insertion sort
concatenate the lists B[0], B[1], …, B[n-1] together in order
时间复杂度
从上面的分析和伪代码我们都可以知道除了桶中排序算法未定,时间复杂度未知以外,其它的时间复杂度都是$\Theta(n)$。因此我们只需要分析桶中使用的算法的时间复杂度就好了。
假如我们调用的是插入排序,假设$n_i$是表示桶B[i]中元素个数(大于等于0)。因为插入排序的时间复杂度为$O(n^2)$,所以桶排序的时间为:
$T(n)=\Theta(n)+\Sigma_{i=0}^{n-1}{O(n_i^2)}$
平均运行时间:
$E[T(n)]=E[\Theta(n)+\Sigma_{i=0}^{n-1}{O(n_i^2}]$
$=\Theta(n)+\Sigma_{i=0}^{n-1}{E[O(n_i^2)]}$
$=\Theta(n)+\Sigma_{i=0}^{n-1}{O(E[n_i^2])}$
经过一系列的数学转换我们可以得到
$E[n_i^2]=2-1/n$
代入上式得到:
$E[T(n)]=\Theta(n)+n\cdot O(2-1/n)=\Theta(n)$
到此我们可以得到一个结论:桶排序可以在线性时间内完成必须要满足的条件是:所有桶的大小的平方与总的元素数呈线性关系。
我们假设极限条件只有一个桶,那么 $n^2与n$ 绝对不可能是线性关系;假设另一个极限,每个桶中刚好一个元素,那么就是 $n与n$ 刚好呈线性关系。所以输入数据可以不服从均匀分布,但是如果要达到线性条件的标准,那么输入数据一定是分散均匀的。
参考资料
- https://baike.baidu.com/item/%E8%AE%A1%E6%95%B0%E6%8E%92%E5%BA%8F
- https://baike.baidu.com/item/%E5%9F%BA%E6%95%B0%E6%8E%92%E5%BA%8F
- https://baike.baidu.com/item/%E6%A1%B6%E6%8E%92%E5%BA%8F
- https://www.byvoid.com/zhs/blog/sort-radix
- https://blog.csdn.net/u012243115/article/details/47172787
- https://pan.baidu.com/s/1u1Q_359Oq42zz4sKtURVwA
