题目一:Longest Substring Without Repeating Characters
题目描述
Given a string, find the length of the longest substring without repeating characters.
Example 1:
Input: "abcabcbb" Output: 3 Explanation: The answer is "abc", with the length of 3.Example 2:
Input: "bbbbb" Output: 1 Explanation: The answer is "b", with the length of 1.Example 3:
Input: "pwwkew" Output: 3 Explanation: The answer is "wke", with the length of 3. Note that the answer must be a substring, "pwke" is a subsequence and not a substring.
题目给出一个字符串,要求找出其最长字符不重复子串。注意子串和子序列的区别。
我的解法
动态规划
这道题目对于我来说,想出解决思路并不难,但是想要实现我却没有办法。想了好久才试了一下用python,结果就通过了。
我的思路就是动态规划,nums[i]表示的是字符串中以s[i+1]结尾的最长不重复子串长度,把字符串遍历完也即得到了完整的nums列表,列表中的最大值就是我们需要的答案。
subs是保存最长子字符串中字符的列表。首先我们初始化nums[0] = 0,subs = [],然后从左到右依次遍历字符串s:
nums[i+1] = nums[i] + 1 if s[i] not in subssubs = subs[index+1:], nums[i+1] = len(subs) + 1if s[i] in subs, index = findIndex(subs, s[i])- 最后再将当前字符加入列表subs,继续遍历下一字符
class Solution:
def findIndex(self, s: str, char) -> int:
for index, c in enumerate(s):
if c == char:
return index
return -1
def lengthOfLongestSubstring(self, s: str) -> int:
subs = list()
nums = [0]
for i,char in enumerate(s):
index = self.findIndex(subs, char)
if index == -1:
nums.append(nums[i] + 1)
subs.append(char)
else:
subs = subs[index+1:]
nums.append(len(subs) + 1)
subs.append(char)
return max(nums)
他人解法
滑动窗口法
我们使用集合存储当前字符到滑动窗口[i, j)中(初始状态i == j),然后我们将下标j向右移动,如果s[j]不在滑动窗口中,我们将其加入滑动窗口,并将j继续向右移动,直到s[j]在滑动窗口中。这时我们已经得到了当前最长不重复子串长度j-i,我们需要不断地把s[i]移出滑动窗口,并将i++自加,直到s[j]不在当前滑动窗口中。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int n = s.length();
set<char> chars;
int i = 0, j = 0, maxLen = 0;
while (i < n && j < n) {
if (chars.count(s[j])) {
chars.erase(s[i++]);
} else {
chars.insert(s[j++]);
maxLen = max(maxLen, j - i);
}
}
return maxLen;
}
};
滑动窗口优化
上面的方法如果发现s[j]存在于当前滑动窗口中时,由于不知道等于s[j]的那个字符的具体下标,因此只能依次从滑动窗口左边开始删掉字符,直到s[j]不存在当前的滑动窗口中。
如果我们一开始就把字符及其下标存好,那么就不需要这么麻烦一个一个删除了。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int n = s.length(), maxLen = 0;
map<char, int> chars;
for (int i = 0, j = 0; j < n; j++) {
if (chars.find(s[j]) != chars.end()) { //find it
i = max(i, chars.at(s[j]));
}
maxLen = max(maxLen, j - i + 1);
chars[s[j]] = j + 1;
}
return maxLen;
}
};
ASCII法
本质上还是哈希表。如果我们知道字符集很小,则可以使用整数数组作为直接访问表替换Map。常用的访问表有:
int[26]for Letters ‘a’ - ‘z’ or ‘A’ - ‘Z’int[128]for ASCIIint[256]for Extended ASCII
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int n = s.length(), maxLen = 0;
int chars[128];
for (int i = 0; i < 128; i++) {
chars[i] = 0;
}
for (int i = 0, j = 0; j < n; j++) {
i = max(i, chars[s[j]]);
maxLen = max(maxLen, j - i + 1);
chars[s[j]] = j + 1;
}
return maxLen;
}
};
题目二:Longest Palindromic Substring
题目描述
Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.
Example 1:
Input: "babad" Output: "bab" Note: "aba" is also a valid answer.Example 2:
Input: "cbbd" Output: "bb"
题目给出一个字符串,要求我们求出该字符串的最长回文子串。注意子串和子序列的区别。
我的解法
第二次做这道题,没想到我的第一想法竟然是马拉车算法。
具体分析看我的这篇文章:Leetcode刷题之Dynamic-Programming 第一题
class Solution {
public:
string longestPalindrome(string s) {
if (s.size() < 2) return s;
string ss = "#";
for (int i = 0; i < s.size(); i++) {
ss += s.substr(i,1) + "#";
}
int mid = 0, right = 0, maxMid = 0, maxLen = 0;
vector<int> dp(ss.size(), 0);
for (int i = 1; i < ss.size(); i++) {
if (i < right) {
int ii = 2 * mid - i;
if (ii >= 0) {
dp[i] = min(dp[ii], right - i);
}
}
while (i-dp[i]-1 >= 0 && i+dp[i]+1 < ss.size() && ss[i-dp[i]-1] == ss[i+dp[i]+1]) {
dp[i]++;
}
if (right < i + dp[i] ) {
right = i + dp[i];
mid = i;
}
if (maxLen < dp[i]) {
maxLen = dp[i];
maxMid = i;
}
}
int start = (maxMid - maxLen) / 2;
return s.substr(start, maxLen);
}
};
他人解法
上一篇文章已经介绍了其他人的解法,所以这次我们就来看看这道题目本身的solution
Approach 1: Longest Common Substring
Common mistake
Some people will be tempted to come up with a quick solution, which is unfortunately flawed (however can be corrected easily):
Reverse SS and become S’S′. Find the longest common substring between SS and S’S′, which must also be the longest palindromic substring.
This seemed to work, let’s see some examples below.
For example, SS = “caba”, S’S′ = “abac”.
The longest common substring between SS and S’S′ is “aba”, which is the answer.
Let’s try another example: SS = “abacdfgdcaba”, S’S′ = “abacdgfdcaba”.
The longest common substring between SS and S’S′ is “abacd”. Clearly, this is not a valid palindrome.
Algorithm
We could see that the longest common substring method fails when there exists a reversed copy of a non-palindromic substring in some other part of SS. To rectify this, each time we find a longest common substring candidate, we check if the substring’s indices are the same as the reversed substring’s original indices. If it is, then we attempt to update the longest palindrome found so far; if not, we skip this and find the next candidate.
This gives us an O(n^2) Dynamic Programming solution which uses O(n^2) space (could be improved to use O(n) space).
这里我实现了一个最长公共子串的解法,实在是太慢了
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
vector<vector<int>> dp(n+1, vector(n+1, 0));
string ss = s;
reverse(ss.begin(), ss.end());
int start = 0, maxLen = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (s[i-1] == ss[j-1]) {
dp[i][j] = dp[i-1][j-1] + 1;
}
if (maxLen < dp[i][j]) {
int ii = i - dp[i][j];
int jj = j - dp[i][j];
if (ii + j == n-1 && i + jj == n-1) { //check if the same place
maxLen = dp[i][j];
start = ii;
}
//else keep the dp[i][j]
}
}
}
return s.substr(start, maxLen+1);
}
};
Approach 2: Brute Force
Approach 3: Dynamic Programming
Approach 4: Expand Around Center
In fact, we could solve it in O(n^2) time using only constant space.
We observe that a palindrome mirrors around its center. Therefore, a palindrome can be expanded from its center, and there are only 2n - 1 such centers.
You might be asking why there are 2n - 1 but not nn centers? The reason is the center of a palindrome can be in between two letters. Such palindromes have even number of letters (such as “abba”) and its center are between the two ‘b’s.
Complexity Analysis
- Time complexity : O(n^2). Since expanding a palindrome around its center could take O(n) time, the overall complexity is O(n^2).
- Space complexity : O(1).
Approach 5: Manacher’s Algorithm
There is even an O(n) algorithm called Manacher’s algorithm, explained here in detail. However, it is a non-trivial algorithm, and no one expects you to come up with this algorithm in a 45 minutes coding session. But, please go ahead and understand it, I promise it will be a lot of fun.
没想到马拉车算法这么难,我居然只想到用马拉车算法。
题目三:ZigZag Conversion
题目描述
The string
"PAYPALISHIRING"is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)P A H N A P L S I I G Y I RAnd then read line by line:
"PAHNAPLSIIGYIR"Write the code that will take a string and make this conversion given a number of rows:
string convert(string s, int numRows);Example 1:
Input: s = "PAYPALISHIRING", numRows = 3 Output: "PAHNAPLSIIGYIR"Example 2:
Input: s = "PAYPALISHIRING", numRows = 4 Output: "PINALSIGYAHRPI" Explanation: P I N A L S I G Y A H R P I
题目给出一个字符串s和一个整数numRows,要求将该字符串中的字符从左到右按纵向的顺序依次排成一个numRows行的Z字形,然后再将每一行的字符串起来,组成一个新的字符串。要求返回新的字符串。
我的解法
顺序遍历,按行成子串
说实话,我实在想不出来这道题出来有什么用呢。难怪那么多人投反对票。刚开始我也没想到怎么做,字符串的题目也太稀奇古怪了吧!我是看了solution才写出来的。
该思路就是有多少行就定义多少个子字符串,依次遍历原字符串将字符一个一个加到对应的子字符串上,最后在将所有的子字符串接在一起就是最终的结果。
时间复杂度和空间复杂度O(n)
class Solution {
public:
string convert(string s, int numRows) {
if (1 == numRows) return s;
bool goDown = false;
vector<string> rows(min(numRows, int(s.size())));
int curRow = 0;
for (char c : s) {
rows[curRow] += c;
if (0 == curRow || curRow == numRows-1) {
goDown = !goDown;
}
curRow = goDown ? curRow + 1 : curRow - 1;
}
string ret;
for (string s : rows) {
ret += s;
}
return ret;
}
};
他人解法
大部分人都是用上面的子串法,很少有人认为这是一道数学问题
逐行扫描法

首先我们找出字符之间位置的统计规律:
第一行和最后一行比较特殊,我们先找出他们的位置规律(i是当前行号,k是当前行的第k+1个字符):
- 第一行的各个字符在原字符串中的索引是
k * ( 2 * numRows - 2 ) - 最后一行的各个字符在原字符串中的索引是
k * ( 2 * numRows - 2 ) + numRows - 1
然后我们再来看中间行,中间行我们注意到有两个不同的点,一个位于斜线上,一个位于竖线上。那么显然这两种情况我们必须分开讨论。
竖线上的好办,为什么呢?因为竖线的最顶上我们已经知道位置了。而竖线的最顶上又是竖线的起点,所以竖线上的点的索引就是竖线上顶点的索引加上偏移(所在行号)。即:
- 中间行的竖线上的字符在原字符串中的索引为
k * ( 2 * numRows - 2 ) + i
由于是先有竖线后有斜线,所以我们就根据竖线的字符位置去推算斜线的字符位置,容易看出相邻竖线与斜线上的字符之间的索引偏移跟其所在行号有关。偏移为:2 * (numRows - i) - 2,所以:
k * ( 2 * numRows - 2 ) + i + 2 * (numRows - i) - 2 = (k+1)(2 * numRows - 2) - i
- 中间行的斜线上的字符在原字符串中的索引为
(k+1)(2 * numRows - 2) - i
class Solution {
public:
string convert(string s, int numRows) {
if (1 == numRows) return s;
string ret = "";
int step = 2 * numRows - 2;
for (int i = 0; i < numRows; i++) {
for (int j = 0; i+j < s.size(); j += step) {
ret += s[j+i]; //竖线的统一一个公式
if (0 != i && numRows-1 != i && j+step-i < s.size()) {
ret += s[j+step-i];
}
}
}
return ret;
}
};
题目四:String to Integer (atoi)
题目描述
Implement
atoiwhich converts a string to an integer.The function first discards as many whitespace characters as necessary until the first non-whitespace character is found. Then, starting from this character, takes an optional initial plus or minus sign followed by as many numerical digits as possible, and interprets them as a numerical value.
The string can contain additional characters after those that form the integral number, which are ignored and have no effect on the behavior of this function.
If the first sequence of non-whitespace characters in str is not a valid integral number, or if no such sequence exists because either str is empty or it contains only whitespace characters, no conversion is performed.
If no valid conversion could be performed, a zero value is returned.
Note:
- Only the space character
' 'is considered as whitespace character.- Assume we are dealing with an environment which could only store integers within the 32-bit signed integer range: [−231, 231 − 1]. If the numerical value is out of the range of representable values, INT_MAX (231 − 1) or INT_MIN (−231) is returned.
Example 1:
Input: "42" Output: 42Example 2:
Input: " -42" Output: -42 Explanation: The first non-whitespace character is '-', which is the minus sign. Then take as many numerical digits as possible, which gets 42.Example 3:
Input: "4193 with words" Output: 4193 Explanation: Conversion stops at digit '3' as the next character is not a numerical digit.Example 4:
Input: "words and 987" Output: 0 Explanation: The first non-whitespace character is 'w', which is not a numerical digit or a +/- sign. Therefore no valid conversion could be performed.Example 5:
Input: "-91283472332" Output: -2147483648 Explanation: The number "-91283472332" is out of the range of a 32-bit signed integer. Thefore INT_MIN (−231) is returned.
题目给出一个字符串,按要求将其转化成int型的整数
我的解法
题目真是像评论区里所言,像狗屎一样。当你以为能够通过的时候它总是会冒出一些稀奇古怪的输入。这也还好,通过不断地提交总能避免(难怪有人说这道题目不是考算法,而是考if-else的熟练运用)。但是,测试的例子能通过,提交的时候同一个例子就卡住了,这我能怎么办?
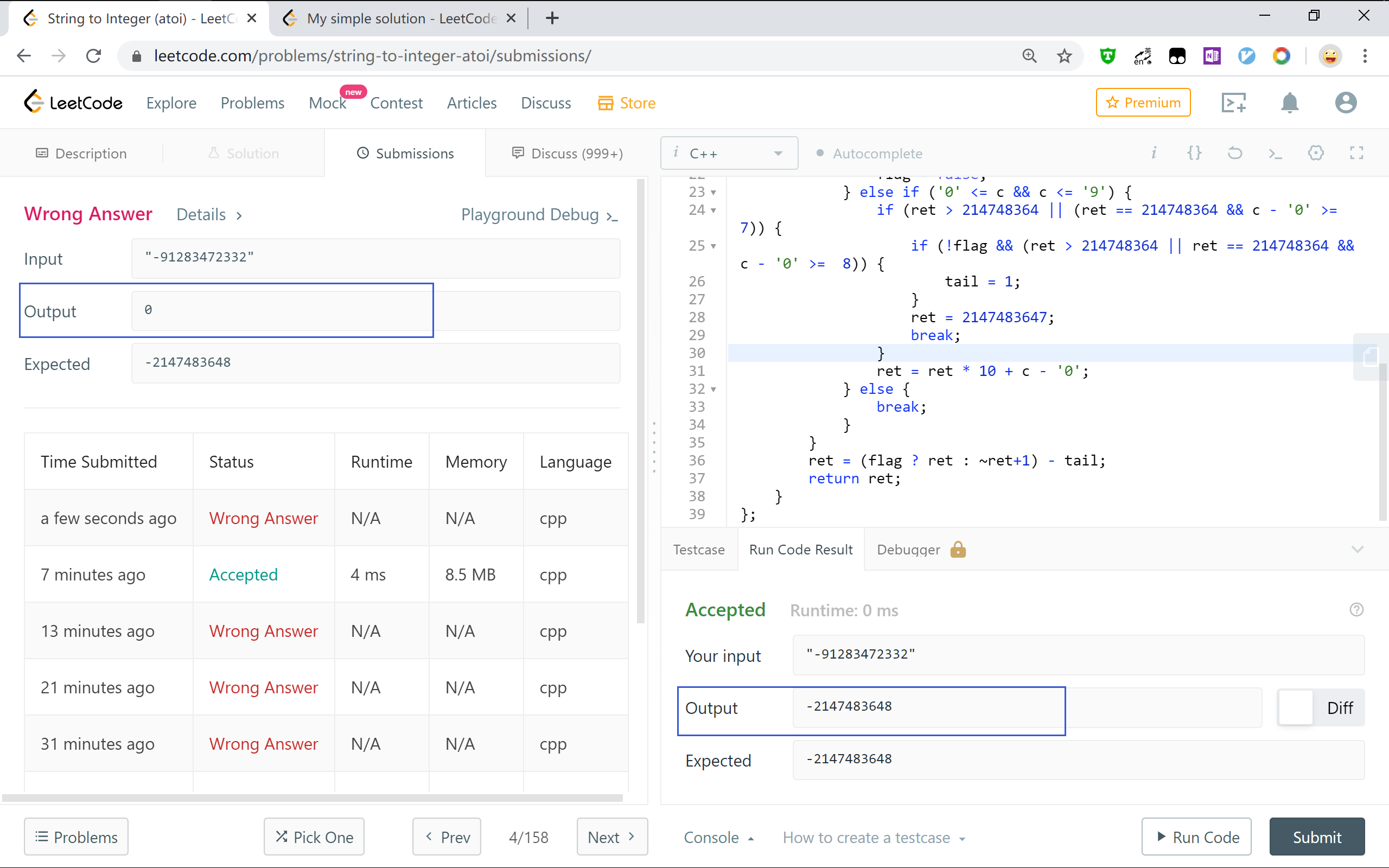
class Solution {
public:
int myAtoi(string str) {
int ret = 0;
int tail = 0;
bool flag = true;
char start;
for (char c : str) {
if (' ' == c) {
continue;
} else if ('+' == c) {
if (start == '+' || start == '-') {
break;
}
start = '+';
continue;
} else if ('-' == c) {
if (start == '+' || start == '-') {
break;
}
start = '-';
flag = false;
} else if ('0' <= c && c <= '9') {
if (ret > 214748364 || (ret == 214748364 && c - '0' >= 7)) {
if (!flag && (ret > 214748364 || ret == 214748364 && c - '0' >= 8)) {
tail = 1;
}
ret = 2147483647;
break;
}
ret = ret * 10 + c - '0';
} else {
break;
}
}
ret = (flag ? ret : ~ret+1) - tail;
return ret;
}
};
他人解法
不解释了。刚开始看见题目评分那么低我本来不打算做的,但是我想着增长一下见识才一股脑做了。
class Solution {
public:
int myAtoi(string str) {
int sign = 1, base = 0, i = 0;
while (str[i] == ' ') { i++; }
if (str[i] == '-' || str[i] == '+') {
sign = 1 - 2 * (str[i++] == '-');
}
while (str[i] >= '0' && str[i] <= '9') {
if (base > INT_MAX / 10 || (base == INT_MAX / 10 && str[i] - '0' > 7)) {
if (sign == 1) return INT_MAX;
else return INT_MIN;
}
base = 10 * base + (str[i++] - '0');
}
return base * sign;
}
};
题目五:Regular Expression Matching
题目描述
Given an input string (
s) and a pattern (p), implement regular expression matching with support for'.'and'*'.'.' Matches any single character. '*' Matches zero or more of the preceding element.The matching should cover the entire input string (not partial).
Note:
scould be empty and contains only lowercase lettersa-z.pcould be empty and contains only lowercase lettersa-z, and characters like.or*.Example 1:
Input: s = "aa" p = "a" Output: false Explanation: "a" does not match the entire string "aa".Example 2:
Input: s = "aa" p = "a*" Output: true Explanation: '*' means zero or more of the preceding element, 'a'. Therefore, by repeating 'a' once, it becomes "aa".Example 3:
Input: s = "ab" p = ".*" Output: true Explanation: ".*" means "zero or more (*) of any character (.)".Example 4:
Input: s = "aab" p = "c*a*b" Output: true Explanation: c can be repeated 0 times, a can be repeated 1 time. Therefore, it matches "aab".Example 5:
Input: s = "mississippi" p = "mis*is*p*." Output: false
题目给出一个字符串s和模式字符串p,要求判断二者是否匹配。
具体的分析可以回顾我之前的一篇文章的第二题:Leetcode刷题之Dynamic Programming
我的解法
我的第一想法是递归,第二想法是动态规划,毕竟之前就做过这道题目。因为递归实现起来比较简单,所以我就先用递归再实现了一遍。思路虽然不算难,但再次实现的过程却有点坎坷,经过多次debug才顺利通过
递归
class Solution {
public:
bool isMatch(string s, string p) {
if (p.empty()) return s.empty();
if ('*' == p[1]) {
return isMatch(s, p.substr(2)) || (!s.empty() && (s[0] == p[0] || '.' == p[0]) && isMatch(s.substr(1), p));
} else {
return !s.empty() && (s[0] == p[0] || '.' == p[0]) && isMatch(s.substr(1), p.substr(1));
}
}
};
迭代
和递归的思路一致,但用迭代来实现的话,就属于动态规划的范畴了。以下代码我很快就写出了整体框架,可就是怎么都通不过去,看了之前的代码才明白原来边界条件没注意。即dp[0][j] = j>1 && '*' == p[j-1] && dp[0][j-2];,该边界条件代表的意思是当字符串为空时,只要模式字符串里有*,那么两者还是有可能匹配。匹配得到的结果在(dp[i-1][j] && (s[i-1] == p[j-2] || '.' == p[j-2]));中得到利用。
class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size(), n = p.size();
vector<vector<bool>> dp(m+1, vector(n+1, false));
dp[0][0] = true;
for (int j = 1; j <= n; j++) {
dp[0][j] = j>1 && '*' == p[j-1] && dp[0][j-2];
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if ('*' == p[j-1]) {
dp[i][j] = dp[i][j-2] || (dp[i-1][j] && (s[i-1] == p[j-2] || '.' == p[j-2]));
} else {
dp[i][j] = dp[i-1][j-1] && (s[i-1] == p[j-1] || '.' == p[j-1]);
}
}
}
return dp[m][n];
}
};
题目六:Integer to Roman
题目描述
Roman numerals are represented by seven different symbols:
I,V,X,L,C,DandM.Symbol Value I 1 V 5 X 10 L 50 C 100 D 500 M 1000For example, two is written as
IIin Roman numeral, just two one’s added together. Twelve is written as,XII, which is simplyX+II. The number twenty seven is written asXXVII, which isXX+V+II.Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not
IIII. Instead, the number four is written asIV. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written asIX. There are six instances where subtraction is used:
Ican be placed beforeV(5) andX(10) to make 4 and 9.Xcan be placed beforeL(50) andC(100) to make 40 and 90.Ccan be placed beforeD(500) andM(1000) to make 400 and 900.Given an integer, convert it to a roman numeral. Input is guaranteed to be within the range from 1 to 3999.
Example 1:
Input: 3 Output: "III"Example 2:
Input: 4 Output: "IV"Example 3:
Input: 9 Output: "IX"Example 4:
Input: 58 Output: "LVIII" Explanation: L = 50, V = 5, III = 3.Example 5:
Input: 1994 Output: "MCMXCIV" Explanation: M = 1000, CM = 900, XC = 90 and IV = 4.
题目给出一个范围是1-3999的整数,要我们将其转化成罗马数字。
我的解法
我的解法很简单,就是从最大的单位开始判断,其中1开头的单位都用while循环判断,因为可能是多个组合在一起,但是其它的都不可能是多个,所以都只需要用if判断一遍就好了。整体下来把num减到0就能得到最终的结果了。
class Solution {
public:
string intToRoman(int num) {
string ret = "";
while (num >= 1000) {
ret += "M";
num -= 1000;
}
if (num >= 900) {
ret += "CM";
num -= 900;
}
if (num >= 500) {
ret += "D";
num -= 500;
}
if (num >= 400) {
ret += "CD";
num -= 400;
}
while (num >= 100) {
ret += "C";
num -= 100;
}
if (num >= 90) {
ret += "XC";
num -= 90;
}
if (num >= 50) {
ret += "L";
num -= 50;
}
if (num >= 40) {
ret += "XL";
num -= 40;
}
while (num >= 10) {
ret += "X";
num -= 10;
}
if (num >= 9) {
ret += "IX";
num -= 9;
}
if (num >= 5) {
ret += "V";
num -= 5;
}
if (num >= 4) {
ret += "IV";
num -= 4;
}
while (num >= 1) {
ret += "I";
num -= 1;
}
return ret;
}
};
他人解法
别人就聪明了,虽然说本质上来说我们是同一种算法,但别人更聪明,他们把特殊的整数和与之对应的罗马符号分别存储了下来:
class Solution {
public:
string intToRoman(int num) {
string res;
string sym[] = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};
int val[] = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};
for(int i=0; num != 0; i++) {
while(num >= val[i]) {
num -= val[i];
res += sym[i];
}
}
return res;
}
};
题目七:Roman to Integer
题目描述
Roman numerals are represented by seven different symbols:
I,V,X,L,C,DandM.Symbol Value I 1 V 5 X 10 L 50 C 100 D 500 M 1000For example, two is written as
IIin Roman numeral, just two one’s added together. Twelve is written as,XII, which is simplyX+II. The number twenty seven is written asXXVII, which isXX+V+II.Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not
IIII. Instead, the number four is written asIV. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written asIX. There are six instances where subtraction is used:
Ican be placed beforeV(5) andX(10) to make 4 and 9.Xcan be placed beforeL(50) andC(100) to make 40 and 90.Ccan be placed beforeD(500) andM(1000) to make 400 and 900.Given a roman numeral, convert it to an integer. Input is guaranteed to be within the range from 1 to 3999.
Example 1:
Input: "III" Output: 3Example 2:
Input: "IV" Output: 4Example 3:
Input: "IX" Output: 9Example 4:
Input: "LVIII" Output: 58 Explanation: L = 50, V= 5, III = 3.Example 5:
Input: "MCMXCIV" Output: 1994 Explanation: M = 1000, CM = 900, XC = 90 and IV = 4.
题目给出一个代表一个整数的由罗马符号组成的字符串,要求我们将其转化成整数。
我的解法
为什么Integer to Roman是medium难度,而Roman to Integer却是easy难度呢?毕竟我自己做题的感觉是第一题我一下子就写出来了,而这道题我是错了两次才好不容易写出来的。
有了上一题的经验,这一题我就是借鉴上一题别人的做法,先使用数组将特定的整数及其对应的罗马数字存储起来。然后再从左到右依次遍历字符串去比对。
class Solution {
public:
int romanToInt(string s) {
int value[] = {1000,900,500,400,100,90,50,40,10,9,5,4,1};
string ss[] = {"M","CM","D","CD","C","XC","L","XL","X","IX","V","IV","I"};
int ret = 0;
for (int i = 0, j = 0; i < 13 && j < s.size(); i++) {
while (true) {
if (s.substr(j,1) == ss[i] ) {
j++;
ret += value[i];
}
else if (s.substr(j,2) == ss[i]) {
j += 2;
ret += value[i];
} else {
break;
}
}
}
return ret;
}
};
他人解法
别人的解法就五花八门了!
解法一
从右到左一次扫描得到结果,过程采用switch case分支处理
class Solution {
public:
int romanToInt(string s) {
int res = 0;
for (int i = s.length()-1; i >= 0; i--) {
char c = s[i];
switch (c) {
case 'I':
res += (res >= 5 ? -1 : 1);
break;
case 'V':
res += 5;
break;
case 'X':
res += 10 * (res >= 50 ? -1 : 1);
break;
case 'L':
res += 50;
break;
case 'C':
res += 100 * (res >= 500 ? -1 : 1);
break;
case 'D':
res += 500;
break;
case 'M':
res += 1000;
break;
}
}
return res;
}
};
解法二
先减一遍再加一遍
class Solution {
public:
int romanToInt(string s) {
int sum=0;
for (int i = 0; i < s.length(); i++) {
if(s.substr(i,2) == "IV") {sum-=2;}
if(s.substr(i,2) == "IX") {sum-=2;}
if(s.substr(i,2) == "XL") {sum-=20;}
if(s.substr(i,2) == "XC") {sum-=20;}
if(s.substr(i,2) == "CD") {sum-=200;}
if(s.substr(i,2) == "CM") {sum-=200;}
}
for(char c : s) {
if(c == 'M') sum+=1000;
if(c == 'D') sum+=500;
if(c == 'C') sum+=100;
if(c == 'L') sum+=50;
if(c == 'X') sum+=10;
if(c == 'V') sum+=5;
if(c == 'I') sum+=1;
}
return sum;
}
};
题目八:Longest Common Prefix
题目描述
Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string
"".Example 1:
Input: ["flower","flow","flight"] Output: "fl"Example 2:
Input: ["dog","racecar","car"] Output: "" Explanation: There is no common prefix among the input strings.Note:
All given inputs are in lowercase letters
a-z.
题目给出一个字符串数组,要求数组中各个字符串的最长公共前缀。
我的解法
k轮遍历所有字符串
就是单纯地从每一个字符串地第一个字符开始比较,如果有字符串长度不足或者是字符不相等的情况就停止,返回之前匹配地最长公共前缀。(运气好,一次写完通过)
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
int n = strs.size();
if (0 == n) return "";
if (1 == n) return strs[0];
bool flag = true;
int end = -1;
while (flag) {
end++;
char c = strs[0][end];
for (int i = 0; i < n; i++) {
if (end >= strs[i].size() || strs[i][end] != c) {
flag = false;
break;
}
}
}
return strs[0].substr(0, end);
}
};
他人解法
一轮遍历strs中所有字符串
以第一个字符串为基准,遍历并比较剩余的字符串。
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
int n = strs.size();
if (0 == n) return "";
string ret = strs[0];
for (int i = 1; i < strs.size(); i++) {
int end = 0;
while (end < ret.size() && end < strs[i].size()) {
if (ret[end] != strs[i][end]) {
break;
}
end++;
}
ret = ret.substr(0, end);
}
return ret;
}
};
排序后比较两端字符串
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
int n = strs.size();
if(0 == n) return "";
string res;
sort(strs.begin(), strs.end());// sort the array
string first = strs[0]; // first word
string last = strs[n-1];// last word
int limit = min(first.length(), last.length());
for(int i = 0; i < limit; i++) {// find out the longest common prefix between first and last word
if(first[i] == last[i]) {
res += first[i];
} else {
break;
}
}
return res;
}
};
题目九:Letter Combinations of a Phone Number
题目描述
Given a string containing digits from
2-9inclusive, return all possible letter combinations that the number could represent.A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
Example:
Input: "23" Output: ["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].Note:
Although the above answer is in lexicographical order, your answer could be in any order you want.
题目给出一个由2-9组成的字符串,每个数字表示普通手机键盘九键上对应的几个字符,要求返回该字符串所表示的所有可能字符串。
我的解法
扩散法
其实这就是不断地做笛卡尔积,但是给出的数字字符串长度又不一定,所以肯定不能蛮力使用多个for循环破解。
我这里是将每个数字看成一个字符的集合,我们要做的就是求这些数字代表的集合的笛卡尔积。我这里的实现是类似于病毒扩散
首先按顺序从每个集合取出第一个字符组成一个字符串s存在一个容器ret中,这个字符串的长度就是集合的个数,因此其也是我们所求字符串中的一个。我们接下来就用该字符串来产出其它字符串,最终得到正确结果:
- 按顺序对每一个集合,遍历除了第一个字符之外的剩余的其它字符(第一个字符已经集中在s中)
- 对于每一个字符,将当前ret容器中的字符串的对应位置替换为该字符从而得到新的字符串并加入到ret容器中。
class Solution {
public:
vector<string> letterCombinations(string digits) {
vector<string> ret, phone;
string temp;
int n = digits.size();
if (0 == n) return ret;
phone = {"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
for (int i = 0; i < n; i++) {
temp += phone[digits[i]-'2'][0];
}
ret.push_back(temp);
for (int i = 0; i < n; i++) {
int retSize = ret.size();
string letters = phone[digits[i]-'2'];
for (int j = 1; j < letters.size(); j++) {
for (int k = 0; k < retSize; k++) {
temp = ret[k];
temp[i] = letters[j];
ret.push_back(temp);
}
}
}
return ret;
}
};
他人解法
回溯法
The stack trace would look like that for example where “»” means push (= go forward) and “«” means pop (= backtrack). Then finally, “[ ]” means we found a valid combination.
Root » “a” » “ad” » [“adg”] « “ad” » [“adh”] « “ad” » [“adi”] « “ad” « “a” « Root » “b” » “bd” » [“bdg”] « “bd” » [“bdh”] « “bd” » [“bdi”] « “bd” « “b” « Root » “c” » etc.
That’s how we backtrack in this solution.
class Solution {
map<char, string> phone = {
{'2', "abc"},
{'3', "def"},
{'4', "ghi"},
{'5', "jkl"},
{'6', "mno"},
{'7', "pqrs"},
{'8', "tuv"},
{'9', "wxyz"},
};
vector<string> output;
public:
void backtrack(string combination, string next_digits) {
if (0 == next_digits.size()) {
output.push_back(combination);
} else {
char digit = next_digits[0];
string letters = phone[digit];
for (int i = 0; i < letters.length(); i++) {
string letter = phone[digit].substr(i, 1);
backtrack(combination + letter, next_digits.substr(1));
}
}
}
vector<string> letterCombinations(string digits) {
if (0 != digits.size()) {
backtrack("", digits);
}
return output;
}
};
累加法
即一个数字一个数字地处理,res里的字符串长度由0不断增长,每处理一个数字就其长度就加一,并且数量也呈倍数增长。每处理一个数字都需要一个空的容器tempRes来辅助处理,处理一个数字后再用tempRes 去更新res。
class Solution {
public:
vector<string> letterCombinations(string digits) {
vector<string> res;
if (digits.empty()) return res;
string charmap[8] = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
res.push_back("");
for (char digit : digits) {
vector<string> tempRes;
string letters = charmap[digit-'2'];
for (char letter : letters) {
for (int i = 0; i < res.size(); i++) {
tempRes.push_back(res[i] + letter);
}
}
res = tempRes;
}
return res;
}
};
题目十:Valid Parentheses
题目描述
Given a string containing just the characters
'(',')','{','}','['and']', determine if the input string is valid.An input string is valid if:
- Open brackets must be closed by the same type of brackets.
- Open brackets must be closed in the correct order.
Note that an empty string is also considered valid.
Example 1:
Input: "()" Output: trueExample 2:
Input: "()[]{}" Output: trueExample 3:
Input: "(]" Output: falseExample 4:
Input: "([)]" Output: falseExample 5:
Input: "{[]}" Output: true
题目给出一个字符串,字符串由大中小括号组成,可以为空。要求判断该字符串中括号是否正确匹配。(其中空字符串表示正确匹配)
我的解法
关于这类的左右匹配题目我已经长记性了,就是用栈来解决。匹配就弹栈,不匹配就压栈。最后检查栈是否为空。为空就返回true,表示匹配,否则就返回false表示不匹配。
class Solution {
public:
bool isValid(string s) {
if (s.empty()) return true;
stack<char> chars;
for (char c : s) {
if (chars.empty()) {
chars.push(c);
} else {
char topest = chars.top();
if ('(' == topest && ')' == c) {
chars.pop();
} else if ('[' == topest && ']' == c) {
chars.pop();
} else if ('{' == topest && '}' == c) {
chars.pop();
} else {
chars.push(c);
}
}
}
return chars.empty();
}
};
他人解法
解法一:栈,存右括号
该解法的作者被人称为‘秀儿’(/狗头),该解法一度让人怀疑人生,接下来让我们去撕开其神秘面纱。
该解法同样是用到栈,但不同于我的解法一股脑地将字符入栈,遇到匹配的再出栈。而是先判断当前字符是左半部分还是右半部分,如果是左半部分那么就将与其匹配的右半部分入栈。如果当前字符是右半部分那么就判断其是否等于当前栈顶字符,如果等于那么就说明匹配了,就弹出栈顶再判断后续字符。如果不等于则说明不匹配,后续的也不用再判断了,可以直接返回false。
给出的字符串判断完毕最后再检查栈是否为空。栈为空才表明匹配完成,否则表示要达到匹配那么还差栈中这些字符。
该解法的优点是大部分情况下不需要遍历整个字符串s就能知道是否匹配。
class Solution {
public:
bool isValid(string s) {
stack<char> chars;
for (char c : s) {
if ('(' == c) {
chars.push(')');
} else if ('[' == c) {
chars.push(']');
} else if ('{' == c) {
chars.push('}');
} else if (chars.empty() || c != chars.top()) {
return false;
} else {
chars.pop(); // c == chars.top()
}
}
return chars.empty();
}
};
解法二:栈,存左括号
class Solution {
public:
bool isValid(string s) {
stack<char> chars;
for (char c : s) {
if ('(' == c || '[' == c || '{' == c) {
chars.push(c);
} else {
if (chars.empty()) return false;
if ('(' == chars.top() && ')' != c) {
return false;
} else if ('[' == chars.top() && ']' != c) {
return false;
} else if ('{' == chars.top() && '}' != c) {
return false;
} else {
chars.pop();
}
}
}
return chars.empty();
}
};
字符串的题目总是让人摸不着头脑,哎!




