Leetcode刷题之Dynamic Programming

zhyjc6于2020-02-08发布 约24488字·约54分钟 本文总阅读量次

题目一：Longest Palindromic Substring

题目描述

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

Example 2:

Input: "cbbd"
Output: "bb"

Accepted

774,554

Submissions

2,706,386

题目给出一个字符串s，要求返回其最长回文子串

我的解法

我的解法很简单，没有用到动态规划的方法，即首先遍历字符串s，每次遍历都将当前字符向两边扩散，得到一个回文子串，然后遍历完成，得到整个字符串的最大回文子串。

我的实现是先实现奇数的回文字符串搜索，然后再同等级地实现一个偶数的最长回文子串搜索。

C++代码

class Solution {
public:
    string longestPalindrome(string s) {
        string maxs = s.substr(0,1);
        int maxlen = 1;
        int n = s.length();
        for (int i = 1; i < n; i++) {
            int j = 1, len = 1;
            while (i - j >= 0 && i + j < n){
                if (s[i-j] == s[i+j]){
                    j++;
                    len += 2; 
                }
                else{
                    break;
                }
            }
            if (maxlen < len){
                maxlen = len;
                int start = i-j<0?0:i-j+1;
                maxs = s.substr(start, maxlen);
            }
        }
        for (int i = maxlen/2; i <= n - maxlen/2; i++){
            int j = 1, len = 0;
            while (i-j+1>=0 && i+j<n){
                if (s[i-j+1] == s[i+j]){
                    len += 2;
                    j++;
                }else{
                    break;
                }
            }
            if (maxlen < len){
                maxlen = len;
                int start = i-j+1<0 ? 0 : i-j+2;
                maxs = s.substr(start, maxlen);
            }
        }
        return maxs;
    }
};

他人解法

别人的解法有几种不同流派。

中心扩展法

下面的解法是 一个for循环遍历（回文串的中间元素），里面嵌套两个while循环，第一个while循环作用是跳过重复元素，第二个while循环是从跳过重复元素后的两边开始扩张，不断比对两头是否相等，不等则退出，得到一个回文串长度，再将之与已经得到的长度比较取其大者；若相等则继续向两边扩张。

这个实现的厉害之处就在于第一个while循环，它不仅仅是跳过了重复元素（减少for循环遍历），还使得我们不用关心回文串的长度是奇数还是偶数

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        int pos, len = 0;
        string longest = s.substr(0,1);
        if (n <= 1){
            return s;
        }
        for (int i = 0; i < n - 1; i++){
            if (n - i <= len / 2){
                break;
            }
            int count = 0;
            while (s[i] == s[i+1] & i < n - 1){
                count++;
                i++;
            }
            int end = i, start = i - count;
            while (start >= 0 && end < n && s[start] == s[end]){
                start--;
                end++;
            }
            if (len < end - start - 2 + 1){
                len = end - start - 1;
                pos = start + 1;
                longest = s.substr(start+1, len);
            }
        }
        return longest;
    }
};

动态规划派

动态规划里出现的题目，那么自然动态规划才是正宗的解题方法。下面的动态规划是自下而上的实现，二维数组isP[i][j]表示子字符串s[i:j]是否是回文串。参考 https://leetcode.com/problems/longest-palindromic-substring/discuss/151144/Bottom-up-DP-Logical-Thinking

原理主要分为三个步骤：

  1. 首先是状态变量

    状态变量为s,e，因为我们在遍历的过程中判断str[s,e]是否为回文串，即state(s,e)==true or false

  2. 其次是目标状态

    我们问题最终所求是字符串中最长的回文串，即max(e - s + 1)

  3. 状态转换

    1. s == e，即单个字符，如”a”是回文串，初始化时处理，state[i][i]=true；
    2. s + 1 == e，两个字符，在1的基础上处理，if(str[s]==str[e]) state[s][e]=true；
    3. s + 2 <= e，三个或以上字符，在2或3的基础上处理, if(state[s+1][e-1] && str[s] == str[e]) state[s][e]=true;；

首先初始化所有元素为true，主要是方便（只要isP[i][i]为true就好了）

然后从右到左遍历所有元素作为子串的start，在选定start的前提下，再以start为基准向右遍历所有字符，作为子串的end，由于isP[i][i]==true，而遍历的基础是上一轮遍历的结果，我们遍历了所有的子串，但是都只遍历一遍，时间复杂度为O(n^2)

class Solution {
public:
    string longestPalindrome(string s) {
        int start = 0, maxLen = 1;
        int n = s.size();
        if (n <= 1){
            return s;
        }
        vector<vector<bool>> isP(n, vector(n,true));
        for (int i = n - 1; i >= 0; i--){
            for (int dist = 1; dist < n - i; dist++){
                int j = i + dist;
                if (dist == 1){
                    isP[i][j] = s[i]==s[j];
                }else{
                    isP[i][j] = s[i]==s[j] && isP[i+1][j-1];
                }
                if (isP[i][j] && maxLen < j - i + 1){
                    maxLen = j - i + 1;
                    start = i;
                }
            }
        }
        return s.substr(start, maxLen);
    }
};

马拉车算法派

Manacher Algorithm，最主要优点是时间复杂度为O(n)

马拉车算法其本质上也是动态规划的思想。充分利用了回文串的性质，即关于中心对称。

马拉车算法需要预先在字符串中填充n+1个其它字符，如#，这样就使得得到的新字符串的长度总是奇数n。这样我们就不用考虑回文串的长度是奇数还是偶数了，最后得到的长度是 2*m+1， 对应源字符串长度m

此时我们定义一个数组len[n]，其下标表示新字符串中当前字符的索引（从左到右遍历新字符串），其值为在新字符串中以当前字符为中心的最长回文串的半径（不包括本身）

之后我们定义两组重要变量，第一组是center 和 right，right表示在求数组len的过程中回文串右端到达的最大值（right只会不断增大，即右移），而center则是right对应的回文串的中心字符索引；第二组是start和maxLen，分别表示到目前为止所求的最长回文串在原字符串中的起始下标和最大长度。用于最后的截取最长回文子串。

由以上分析可知，我们只要求得数组len，之后遍历得到其中最大值就可以得到最长回文串了。所以问题就转移到如何求取数组len

这里是马拉车算法的核心，也是动态规划思想的具体体现：

我们从左到右遍历新字符串的过程中，肯定有一个right和center，当我们要求len[i]的时候，我们会看i是在right的哪边

得到最终的len[i]了之后，我们还要更新看情况更新center和right以及start和maxLen

最后，为什么start = (i - maxLen)/2，因为i-maxLen表示的是新字符串最长回文串的起始地址，而我们的新旧字符串的原字符一一对应的关系是new[i] => old[i/2]

而maxLen表示的是新字符串中最长回文串的半径，为什么最后变成最长回文串的长度了呢？这是因为表示半径的时候有一半是其它字符（这里是#），所以其大小直接等于源字符串最长回文字符串的长度。

class Solution {
public:
    string longestPalindrome(string s) {
        if (s.size() <= 1){
            return s;
        }
        string T = "#";
        for (int i = 0; i < s.size(); i++){
            T += s.substr(i,1) + "#";
        }
        int n = T.size();
        vector<int> len(n, 0);
        int center = 0, right = 0, maxLen = 0, start = 0;
        for (int i = 1; i < n - 1; i++){
            int j = 2 * center - i;
            //len[i] = i < right ? min(len[j], i - center) : 0;
            if (i < right){
                if (i + len[j] > right){
                    len[i] = right - i;
                }else{
                    len[i] = len[j];
                }
            }else{
                len[i] = 0;
            }
            while (i-len[i]-1 >= 0 && i+len[i]+1 < n && T[i-len[i]-1] == T[i+len[i]+1]){
                len[i]++;
            }
            if (right < i + len[i]){
                right = i + len[i];
                center = i;
            }
            if (maxLen < len[i]){
                maxLen = len[i];
                start = (i - maxLen) / 2;  // i-maxLen is the start of string T,so it's double of real start
            }
        }
        return s.substr(start, maxLen);   
    }
};

题目二：Regular Expression Matching

题目描述

Given an input string (s) and a pattern (p), implement regular expression matching with support for '.' and '*'.

'.' Matches any single character.
'*' Matches zero or more of the preceding element.

The matching should cover the entire input string (not partial).

Note:

  • s could be empty and contains only lowercase letters a-z.
  • p could be empty and contains only lowercase letters a-z, and characters like . or *.

Example 1:

Input:
s = "aa"
p = "a"
Output: false
Explanation: "a" does not match the entire string "aa".

Example 2:

Input:
s = "aa"
p = "a*"
Output: true
Explanation: '*' means zero or more of the preceding element, 'a'. Therefore, by repeating 'a' once, it becomes "aa".

Example 3:

Input:
s = "ab"
p = ".*"
Output: true
Explanation: ".*" means "zero or more (*) of any character (.)".

Example 4:

Input:
s = "aab"
p = "c*a*b"
Output: true
Explanation: c can be repeated 0 times, a can be repeated 1 time. Therefore, it matches "aab".

Example 5:

Input:
s = "mississippi"
p = "mis*is*p*."
Output: false

题目给出一个字符串s和一个模式字符串p，要求我们判断s和p是否相等。

其中p中包含两个特殊字符. 、*，.可以表示任意字符，很流弊！但是*更流弊，*不能单独存在，它必须跟在一个任意字符（除本身外，包括.）后面，表示这个字符可以出现零次或任意多次。

我的解法

我看到这个一时半会还真想不出怎么做，所以我就看了一下讨论里别人的做法。

这是一个递归的方法，从左到右遍历模式字符串p，首先判断第二个字符是不是*：

  1. 如果是*：由于*表示其前面的字符可以出现零次，所以此时的一种可能是递归函数isMatch(s,p[2:])；另一种可能是字符串s不为空并且s[0]==p[0]或者p[0]=='.'，在这种情况下的递归函数isMatch(s[1:],p)，相当于消去了字符串s的第一个字符。
  2. 如果不是*：那就简单多了，直接比对s和p的第一字符，如果相等或者p的第一字符是.那么就相当于消去了两者的第一个字符，返回递归函数isMatch(s[1:],p[1:])，否则就返回false
  3. 在递归的同时，每次递归第一步就是检查字符串是否为空，但是为什么是先检查模式字符串p呢，这是因为在两者相等的前提下，一定是p先为空，因为p可一次消去两个字符！
class Solution {
public:
    bool isMatch(string s, string p) {
        if (p.empty())    return s.empty();
        if ('*' == p[1])
            return (isMatch(s, p.substr(2)) || !s.empty() && (s[0] == p[0] || '.' == p[0]) && isMatch(s.substr(1), p));
        else
            return !s.empty() && (s[0] == p[0] || '.' == p[0]) && isMatch(s.substr(1), p.substr(1));
        }
};

他人解法

与上述递归思路几乎完全一致，但是非递归，属于标准的动态规划的实现,f[i][j]表示s[0:i-1]与p[0:j-1]是否相等。

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.size(), n = p.size();
        vector<vector<bool>> f(m+1, vector<bool>(n+1, false));
        f[0][0] = true;
        for (int i = 1; i <= n; i++){
            f[0][i] = i > 1 && '*' == p[i - 1] && f[0][i - 2];
        }
        for (int i = 1; i <= m; i++){
            for (int j = 1; j <= n; j++){
                if ('*' == p[j-1]){
                    f[i][j] = f[i][j-2] || (f[i-1][j] && (s[i-1] == p[j-2] || '.' == p[j-2]));
                }else{
                    f[i][j] = f[i-1][j-1] && (s[i-1] == p[j-1] || '.' == p[j-1]);
                }
            }
        }
        return f[m][n];
    }
};

题目三：Longest Valid Parentheses

题目描述

Given a string containing just the characters '(' and ')', find the length of the longest valid (well-formed) parentheses substring.

Example 1:

Input: "(()"
Output: 2
Explanation: The longest valid parentheses substring is "()"

Example 2:

Input: ")()())"
Output: 4
Explanation: The longest valid parentheses substring is "()()"

题目给出一个仅包含左右括号两个字符的字符串，要我们返回最长的括号连续匹配的长度。

我的解法

我这道题目想了好久没想出来。我想到用递归的思路，也想到用动态规划，但是到具体实现的时候遇到了麻烦，没有很连续的思路。思绪也比较杂乱。为了节约时间，我就直接参考别人的做法。

他人解法

解法一

该方法用到了数据结构栈，其实很容易想到，用来存储左括号的索引。定义了一个大小为 n+1 的数组len，len[i]表示字符串s中以s[i-1]字符结尾的最长合法字符串的长度。数组len初始化为0，从左到右扫描字符串s，当遇到右括号并且栈中还有左括号时（栈中的都是未配对的），len[i+1] = i - leftIndex + 1 + len[leftIndex]。leftIndex是左边最近的未配对左括号的索引，s[leftIndex-1]是那个左括号左边的一个字符，可能是左括号也可能是右括号。所以len[leftIndex]可能为零（左括号结尾）也可能不为零。i - leftIndex + 1就是新配对的长度

时间复杂度O(n)

class Solution {
public:
    int longestValidParentheses(string s) {
        int n = s.size();
        stack<int> left_bracktes;
        vector<int> len(n+1, 0);
        int maxLen = 0;
        for (int i = 0; i < n; i++){
            if ('(' == s[i]){
                left_bracktes.push(i);
            }else if (left_bracktes.empty()){
                continue;
            }else{
                int leftIndex = left_bracktes.top();
                len[i + 1] = i - leftIndex + 1 + len[leftIndex];
                if (maxLen < len[i+1]){
                    maxLen = len[i+1];
                }
                left_bracktes.pop();
            }
        }
        return maxLen;
    }
};

解法二

不借助栈。从左到右扫描

for any longest[i], it stores the longest length of valid parentheses which is end at i.

And the DP idea is :

If s[i] is ‘(‘, set longest[i] to 0,because any string end with ‘(‘ cannot be a valid one.

Else if s[i] is ‘)’

If s[i-1] is ‘(‘, longest[i] = longest[i-2] + 2

Else if s[i-1] is ‘)’ and s[i-longest[i-1]-1] == ‘(‘, longest[i] = longest[i-1] + 2 + longest[i-longest[i-1]-2]

For example, input “()(())”, at i = 5, longest array is [0,2,0,0,2,0], longest[5] = longest[4] + 2 + longest[1] = 6.

   int longestValidParentheses(string s) {
            if(s.length() <= 1) return 0;
            int curMax = 0;
            vector<int> longest(s.size(),0);
            for(int i=1; i < s.length(); i++){
                if(s[i] == ')'){
                    if(s[i-1] == '('){
                        longest[i] = (i-2) >= 0 ? (longest[i-2] + 2) : 2;
                        curMax = max(longest[i],curMax);
                    }
                    else{ // if s[i-1] == ')', combine the previous length.
                        if(i-longest[i-1]-1 >= 0 && s[i-longest[i-1]-1] == '('){
                            longest[i] = longest[i-1] + 2 + ((i-longest[i-1]-2 >= 0)?longest[i-longest[i-1]-2]:0);
                            curMax = max(longest[i],curMax);
                        }
                    }
                }
                //else if s[i] == '(', skip it, because longest[i] must be 0
            }
            return curMax;
        }

但是

it is no need to consider the condition “s[i-1] == ‘(‘” since “s[i-longest[i-1]-1] == ‘(‘” actually concludes this case. We could just use “if (i-1>=0 && i-longest[i-1]-1 >=0 && s[i-longest[i-1]-1] == ‘(‘)”

所以可继续化简为

int longestValidParentheses(string s) {
        if(s.length() <= 1) return 0;
        int curMax = 0;
        vector<int> longest(s.size(),0);
        for(int i=1; i < s.length(); i++){
            if(s[i] == ')' && i-longest[i-1]-1 >= 0 && s[i-longest[i-1]-1] == '('){
                    longest[i] = longest[i-1] + 2 + ((i-longest[i-1]-2 >= 0)?longest[i-longest[i-1]-2]:0);
                    curMax = max(longest[i],curMax);
            }
        }
        return curMax;
    }

解法三

借助栈，但是用得更巧。同样从左到右扫描字符串，但是不论是左括号还是右括号都依次入栈（索引入栈而不是元素本身）。每次把栈顶元素与当前元素比较，如果分别是左右括号，则弹出栈顶，得到一个长度i - stk.top()，并实时更新maxL

不得不说真是好巧妙，因为消去的都是合法字符串，剩下的栈顶是刚好消不去的。时间复杂度为O(n)

class Solution {
public:
    int longestValidParentheses(string s) {
        stack<int> stk;
        stk.push(-1);
        int maxL = 0;
        for (int i = 0; i < s.size(); i++) {
            int t = stk.top();
            if(t != -1 && s[i] == ')' && s[t] == '(') {
                stk.pop();
                maxL = max(maxL, i - stk.top());
            }
            else
                stk.push(i);
        }
        return maxL;
    }
};

题目四：Wildcard Matching

题目描述

Given an input string (s) and a pattern (p), implement wildcard pattern matching with support for '?' and '*'.

'?' Matches any single character.
'*' Matches any sequence of characters (including the empty sequence).

The matching should cover the entire input string (not partial).

Note:

  • s could be empty and contains only lowercase letters a-z.
  • p could be empty and contains only lowercase letters a-z, and characters like ? or *.

Example 1:

Input:
s = "aa"
p = "a"
Output: false
Explanation: "a" does not match the entire string "aa".

Example 2:

Input:
s = "aa"
p = "*"
Output: true
Explanation: '*' matches any sequence.

Example 3:

Input:
s = "cb"
p = "?a"
Output: false
Explanation: '?' matches 'c', but the second letter is 'a', which does not match 'b'.

Example 4:

Input:
s = "adceb"
p = "*a*b"
Output: true
Explanation: The first '*' matches the empty sequence, while the second '*' matches the substring "dce".

Example 5:

Input:
s = "acdcb"
p = "a*c?b"
Output: false

题目给出两个字符串s和p，s是任意小写字母组成，p是任意小写字母外加两个特殊字符?和*，但二者都可能为空字符串。其中？匹配任意字符，*匹配任意字符串。要求我们判断s和p是否可能相等。

我的解法

不会做

他人解法

解法一、基于DFS

这个算法实现得比较难以理解，但是思路是比较简单的。

引用算法作者的说明，这其实是一个DFS深度优先搜索算法。主要是因为*是可以匹配任意字符串，假如模式字符串p的*后面的字符是c，但是字符串s中有好几个c，所以*要匹配哪一个字符c之前的字符串呢？从左到右一个一个尝试，每尝试一个直到失败再回过头来尝试下一个，这就是深度优先搜索算法。

class Solution {
public:
 bool isMatch(string s, string p) {
        int i = 0, j = 0;
        int m = s.length(), n = p.length();
        int last_match = -1, starj = -1;
        while (i < m){
            if (j < n && (s[i] == p[j] || p[j] == '?')){
                i++; j++;
            }
            else if (j < n && p[j] == '*'){
                starj = j;
                j++;
                last_match = i;
            }
            else if (starj != -1){
                j = starj + 1;
                last_match++;
                i = last_match;
            }
            else return false;
        }
        while (j < n && '*' == p[j]) j++;
        return j == n;
    }
};

解法二、动态规划

dp[i][j]表示s的前i个字符与p的前j个字符是否匹配。

如果 p[j] 等于 * : dp[i+1][j+1] = dp[i][j+1] || dp[i+1][j] ;

如果 p[j] 不等于 *：dp[i+1][j+1] = dp[i][j] && （s[i] == p[j] || '?' == p[j]）

第二种情况比较容易理解，但是第一种情况则不同。由于*可以匹配任意字符串，当p[j] == '*'时，*如果匹配空字符串，那么dp[i+1][j+1] = dp[i+1][j]，如果*匹配s[i-1]，那么dp[i+1][j+1] = dp[i][j+1]

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.size(), n = p.size();
        vector<vector<bool>> dp(m+1, vector(n+1, false));
        dp[0][0] = true;
        for (int j = 0; j < n; j++){
            dp[0][j+1] = dp[0][j] && '*' == p[j];
        }
        for (int i = 0; i < m; i++){
            for (int j = 0; j < n; j++){
                if ('*' == p[j]){
                    dp[i+1][j+1] = dp[i][j+1] || dp[i+1][j];
                } else {
                    dp[i+1][j+1] = dp[i][j] && (s[i] == p[j] || '?' == p[j]);
                }
            }
        }
        return dp[m][n];
    }
};

题目五：Maximum Subarray

题目描述

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

Follow up:

If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

题目给出一个整型数组nums，要求返回数组中连续元素的和的最大值。

我的解法

动态规划的思想，dp[i]表示数组前i个元素中连续元素的和的最大值。那么有：

最终dp[n]即为所求的值，时间复杂度为O(n)

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n+1, 0);
        dp[0] = 0;
        int max = nums[0];
        for (int i = 0; i < n; i++){
            dp[i+1] = nums[i] + (dp[i] < 0 ? 0 : dp[i]);
            if (max < dp[i+1]){
                max = dp[i+1];
            }
        }
        return max;
    }
};

事实上，没有必要存储每一个dp[i]，因为我们只是从左到右遍历一遍就能得到结果，我们在求一个子问题时只需要上一个子问题的结果，所以我们可以只用一个变量来存储。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int n = nums.size();
        int preSum = nums[0];
        int maxSum = preSum;
        for (int i = 1; i < n; i++){
            preSum = nums[i] + (preSum > 0 ? preSum : 0);
            maxSum = max(preSum, maxSum);
        }
        return maxSum;
    }
};

他人解法

这个解法特别巧妙，其原文是python代码：

for i in range(1, len(nums)):
        if nums[i-1] > 0:
            nums[i] += nums[i-1]
    return max(nums)

源代码就是四行，特别简洁，特别有内涵。下面是我的c++实现

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int maxSum = nums[0];
        for (int i = 1; i < nums.size(); i++){
            if (nums[i-1] > 0){
                nums[i] += nums[i-1];
            }
            if (maxSum < nums[i]){
                maxSum = nums[i];
            }
        }
        return maxSum;
    }
};

该算法除了整型变量maxSum没有其它额外空间，计算结果存储在原nums数组中，nums[i]存储了以nums[i]结尾的所有连续元素的和的最大值。所以计算完后数组中的最大值就是我们所求的值。那么具体是怎么实现的呢？

实际计算根本不用这么麻烦，要计算nums[i]，我们是直接判断nums[i-1]

题目六：Unique Paths

题目描述

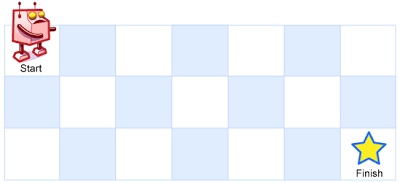
A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

Above is a 7 x 3 grid. How many possible unique paths are there?

题目给出一个m * n的矩形，其中左上角和右下角分别为起点和终点，要求从起点到终点，每次移动只能向右或向下，求所有可能的路线。返回路线总数。

我的解法

由于给出的是图示，这让我们更容易得到动态规划的子问题和子问题之间的联系：

dp[i][j]表示矩形i*j的路线总数。其子问题由图示容易得到是dp[i-1][j]和dp[i][j-1]。dp[i][j] = dp[i-1][j] + dp[i][j-1]

而所有的上边界和左边界的路线都只有一条，即dp[i][1] = dp[1][j] = 1;

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m+1, vector(n+1, 0));
        dp[0][0] = 0;
        for (int i = 1; i <= m; i++){
            dp[i][1] = 1;
        }
        for (int j = 1; j <= n; j++){
            dp[1][j] = 1;
        }
        for (int i = 1; i <= m; i++){
            for (int j = 1; j <= n; j++){
                dp[i][j] = i + j == 2 ? 1 : dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m][n];
    }
};

事实上给出的图表不正好可以作为我们的二维数组吗，我们没必要申请(m+1)*(n+1)的大号数组，因为第一行和第一列是作为基础初始化为1的。此时dp[i][j]表示的是(i+1)*(j+1)的二维数组的总路线。

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m, vector(n, 1));
        for (int i = 1; i < m; i++){
            for (int j = 1; j < n; j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};

他人解法

精简版动态规划

虽然我们定义了一个二维数组，但是一个问题的子问题只有两个，即我们只用到dp[i-1][j]和dp[i][j-1]，所以我们可以通过定义两个一维数组来减少空间利用。

一维数组pre是外层for循环上一轮的cur，相当于dp[i-1][j]，而cur[j-1]就相当于dp[i][j-1]，因为是当前外层循环下的更新。

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int> pre(n, 1), cur(n, 1);
        for (int i = 1; i < m; i++){
            for (int j = 1; j < n; j++){
                cur[j] = pre[j] + cur[j-1];
            }
            swap(cur, pre);
        }
        return pre[n-1];
    }
};

继续优化

上述代码还可以继续优化到只需要使用一个一维数组。因为pre和cur本质上是一个数组的更新前后的两种形态。而我们每次只需要数组中的一个值pre[j]。此时的pre[j]是用来更新cur[j]，而pre[j]实际上又是更新前的cur[j]，所以：

cur[j] += cur[j-1]

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int> cur(n, 1);
        for (int i = 1; i < m; i++){
            for (int j = 1; j < n; j++){
                cur[j] += cur[j-1];
            }
        }
        return cur[n-1];
    }
};

数学公式法

总共m+n-2步，其中向下m-1步，向右n-1步。这所有步的组合总数就是所求总路线数。即组合公式C(m+n-2, m-1) 或 C(m+n-2, n-1)

class Solution {
    public:
        int uniquePaths(int m, int n) {
            int N = n + m - 2;// how much steps we need to do
            int k = m - 1; // number of steps that need to go down
            double res = 1;
            // here we calculate the total possible path number 
            // Combination(N, k) = n! / (k!(n - k)!)
            // reduce the numerator and denominator and get
            // C = ( (n - k + 1) * (n - k + 2) * ... * n ) / k!
            for (int i = 1; i <= k; i++)
                res = res * (N - k + i) / i;
            return (int)res;
        }
    };

题目七：Unique Paths II

题目描述

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and empty space is marked as 1 and 0 respectively in the grid.

Note: m and n will be at most 100.

Example 1:

Input:
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
Output: 2
Explanation:
There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

该题是题目六的延续。题目给出一个m*n的二维数组x，其中的元素1代表障碍，0代表无障碍。机器人从左上角要移动到右下角。在机器人移动的过程中可能会遇到障碍，机器人不能跨越障碍而只能绕过障碍。要求所有可行的路线总数。

我的解法

我的解法非常普通朴素。几乎没有多想就写出来了。思路与第六题一样：

ps: 在这个过程中，我出现了整数加和溢出的情况，最后还是看到了评论区才知道溢出的要当0处理。

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size(), n = obstacleGrid[0].size();
        vector<vector<int>> dp(m, vector(n, 0));
        int flag = 1;
        for (int i = 0; i < m; i++){
            if (obstacleGrid[i][0] == 1){
                flag = 0;
            }
            dp[i][0] = flag;
        }
        flag = 1;
        for (int j = 0; j < n; j++){
            if (obstacleGrid[0][j] == 1){
                flag = 0;
            }
            dp[0][j] = flag;
        }
        for (int i = 1; i < m; i++){
            for (int j = 1; j < n; j++){
                dp[i][j-1] = obstacleGrid[i][j-1] == 1 ? 0 : dp[i][j-1];
                dp[i-1][j] = obstacleGrid[i-1][j] == 1 ? 0 : dp[i-1][j];
                dp[i][j] = dp[i-1][j] > INT_MAX - dp[i][j-1] ? 0 : dp[i-1][j] + dp[i][j-1];
            }
        }
        return obstacleGrid[m-1][n-1] == 1 ? 0 : dp[m-1][n-1];
    }
};

在处理子问题之间的关联时，我们上面是判断子问题是否是因为障碍而为零，最终在判断终点是否是障碍从而得到是否为零。

现在我们不判断子问题，直接判断当前位置是否是障碍从而判断结果是否为零。

for (int i = 1; i < m; i++){
            for (int j = 1; j < n; j++){
                dp[i][j] = obstacleGrid[i][j] == 1 ? 0: (dp[i-1][j] > INT_MAX - dp[i][j-1] ? 0 : dp[i-1][j] + dp[i][j-1]);
            }
        }

他人解法

​ 动态规划

同样是动态规划，为什么别人的就那么简洁。原因在于别人充分利用了二维数组已经初始化为0的特点，只要给出一个引子（dp[0][1] =1或dp[1][0]=1)，就可以利用动态规划犁田式的得到所有值。

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size(), n = obstacleGrid[0].size();
        vector<vector<int>> dp(m+1, vector(n+1, 0));
        dp[0][1] = 1;  //so that dp[1][1] can be 1
        for (int i = 1; i <= m; i++){
            for (int j = 1; j <= n; j++){
                if (!obstacleGrid[i-1][j-1] && dp[i-1][j] < INT_MAX - dp[i][j-1]){
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
                }
            }
        }
        return dp[m][n];
    }
};

题目八：Minimum Path Sum

题目描述

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

Example:

Input:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
Output: 7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.

题目给出一个二维数组，元素皆为非负数。要求以左上角为起点，右下角为终点，得到一条路线，使得路线上所有元素的加和最小。返回这个值。

我的解法

由于该题与上面两题实在是相似，所以我很自然的就写出了代码，也一次性通过。

我的计算都是在题目给出的原数组中实现的，没有使用多余的空间。

grid[i][j]表示以该点为终点的路线加和最小值。由于题目限定只能向下或向右移动，所以可以将其划分为两个子问题：grid[i][j-1]，grid[i-1][j]

grid[i][j] = min(grid[i][j-1], grid[i-1][j])：

边界值：很明显就是第一行和第一列了，边界值由于处于边界所以其子问题只有一个方向：第一行从第二个元素开始其值更新为其前面所有元素的加和；第一列也同样如此。

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int row = grid.size(), col = grid[0].size();
        for (int i = 0; i < row; i++){
            for (int j = 0; j < col; j++){
                if (0 == i && 0 != j){
                    grid[i][j] += grid[i][j-1];
                } else if (0 == j && 0 != i) {
                    grid[i][j] += grid[i-1][j];
                } else if (0 == i && 0 == j){
                    continue;
                } else {
                    grid[i][j] += min(grid[i][j-1], grid[i-1][j]);
                }
            }
        }
        return grid[row-1][col-1];
    }
};

他人解法

利用同样的动态规划空间优化的方法，使得在不动源数据的条件下只额外使用O(n)的空间：

class Solution {
public:
    int minPathSum(vector<vector<int> > &grid) {
        if(!grid.size())return 0;
        const int rows=grid.size(),cols=grid[0].size();
        // r[i] == min path sum to previous row's column i.
        vector<int> r(cols,0);
        int i,j;
        r[0]=grid[0][0];
        for(j=1;j<cols;j++){
            r[j]=grid[0][j]+r[j-1];       
        }
        for(i=1;i<rows;i++){
            r[0]+=grid[i][0];
            for(j=1;j<cols;j++){
                r[j]=min(r[j-1],r[j])+grid[i][j];
            }
        }
        return r[cols-1];
    }
};

题目九：Climbing Stairs

题目描述

You are climbing a stair case. It takes n steps to reach to the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Note: Given n will be a positive integer.

Example 1:

Input: 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 2:

Input: 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

题目给出一个背景：你在爬楼梯，但是你每次只能爬1级或2级，问爬上n级楼梯有多少种爬法？

我的解法

这是很简单的一维动态规划。我们用dp[i]表示爬上i级楼梯有多少种爬法，我们将其划分成两个子问题：

边界值

class Solution {
public:
    int climbStairs(int n) {
        if (1 == n){
            return 1;
        }
        if (2 == n){
            return 2;
        }
        vector<int> dp(n+1, 0);
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++){
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
};

他人解法

使用两个变量代替一维数组dp，将空间复杂度由O(n) 降低到 O(1)

同样是动态规划的空间化简法，使用两个变量依次交替更新达到动态规划的效果。

class Solution {
public:
    int climbStairs(int n) {
        if(n == 1) return 1;
        int f = 1, g = 2;
        for(int i = 3; i <= n; i++) {
            g = f + g;
            f = g - f;
        }
        return g;
    }
};

题目十：Edit Distance

题目描述

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.

You have the following 3 operations permitted on a word:

  1. Insert a character
  2. Delete a character
  3. Replace a character

Example 1:

Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation: 
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')

Example 2:

Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation: 
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')

题目给出两个英文单词word1和word2，要求我们把word1转化为word2，可以使用3种操作方式：

  1. 插入一个字符
  2. 删除一个字符
  3. 替代一个字符

要求任意使用以上三种操作方式，求出把word1转化为word2所需要的最少操作数。

我的解法

这道题我想了很久没有思路。后来是看了高票回答才有思路的。

我们把问题转化为求状态dp[m][n]，其中m、n分别是两个单词的字符串长度。

联想之前做过的爬楼梯，爬到顶层的最后一步可能是两级楼梯也可能是一级楼梯，这里也一样。最后完成匹配的一步可能是delete，可能是insert，也可能是replace。

现在我就来求dp[i][j]:

  1. 如果 word1[i-1] == word2[j-1]：那么dp[i][j] = dp[i-1][j-1]
  2. 而如果word1[i-1] != word2[j-1]：那么问题就可以划分成3种情况了：
    • 字符串word1 instert word2[j-1]，所以dp[i][j] = dp[i][j-1]+ 1
    • 字符串word1 delete word1[i-1]，所以dp[i][j] = dp[i-1][j] + 1
    • 将字符串word1中 word1[i-1] replace 为word2[j-1]，所以dp[i][j] = dp[i-1][j-1] + 1
  3. 我们的最后一步一定是上述情况之一，如果是下面3种情况之一，那么一定是取三者中最小者，因为题目要求是求最小距离。

这四者之间的相对位置如下：

i, j j-1 j
i-1 dp[i-1][j-1] dp[i-1][j]
i dp[i][j-1] dp[i][j]

边界值

注意

为什么在word1[i-1] == word2[j-1]时，dp[i][j]不是等于min(dp[i-1][j-1]，dp[i-1][j]+1，dp[i][j-1] +1)，而是直接等于dp[i-1][j-1]呢？

这是因为在矩阵dp中任意相邻的两个值相差都为1，所以dp[i-1][j-1] <= dp[i-1][j] + 1并且dp[i-1][j-1] <= dp[i][j-1] + 1

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        vector<vector<int>> dp(m+1, vector(n+1, 0));
        for (int i = 1; i <= m; i++){
            dp[i][0] = i;
        }
        for (int j = 1; j <= n; j++){
            dp[0][j] = j;
        }
        for (int i = 1; i <= m; i++){
            for (int j = 1; j <= n; j++){
                if (word1[i-1] == word2[j-1]){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    int min1 = min(dp[i-1][j-1], dp[i-1][j]);
                    dp[i][j] = min(min1, dp[i][j-1]) + 1;
                }
            }
        }
        return dp[m][n];
    }
};

同样我们可以将其化简，使得空间复杂度由O (n^2)将为O(n)

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        vector<int> dp(n+1, 0);
        for (int j = 0; j <= n; j++){
            dp[j] = j;
        }
        for (int i = 1; i <= m; i++){  //m轮更新
            int pre = dp[0];  //更新前的
            dp[0] = i;  //更新
            for (int j = 1; j <= n; j++){
                int temp = dp[j]; //为下一小轮的pre准备
                if (word1[i-1] == word2[j-1]){
                    dp[j] = pre;  //此时的pre = dp[i-1][j-1]
                }else{
                    dp[j] = min(min(pre, dp[j]), dp[j-1]) + 1;
                }
                pre = temp;
            }
        }
        return dp[n];
    }
};

他人解法

递归做法

递归思路无法通过，因为有太多冗余的计算，导致了TLE超出时间限制

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        return dp(word1, word2, m, n);
    }
    int dp(string &word1, string &word2, int n1, int n2){
        if (0 == n1) return n2;
        if (0 == n2) return n1;
        
        if (word1[n1-1] == word2[n2-1]){
            return dp(word1, word2, n1-1, n2-1);
        } else {
            int delete_ = dp(word1, word2, n1-1, n2);
            int insert_ = dp(word1, word2, n1, n2-1);
            int replace_ = dp(word1, word2, n1-1, n2-1);
            return min(min(delete_, insert_), replace_) + 1;
        }
    }
};

递归+打表优化

其实就是在以上递归的基础上遇到冗余的计算就不再计算，而是跳过，从而加快运算速度。

class Solution {
public:
    int table[1001][1001];
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        for (int i = 0; i <= m; i++){
            for (int j = 0; j <= n; j++){
                table[i][j] = -1;
            }
        }
        table[m][n] = dp(word1, word2, m, n);
        return table[m][n];
    }
    int dp(string &word1, string &word2, int n1, int n2){
        if (0 == n1) return n2;
        if (0 == n2) return n1;
        if (-1 != table[n1][n2]){
            return table[n1][n2];
        }
        if (word1[n1-1] == word2[n2-1]){
            table[n1][n2] = dp(word1, word2, n1-1, n2-1);
        } else {
            int delete_ = dp(word1, word2, n1-1, n2);
            int insert_ = dp(word1, word2, n1, n2-1);
            int replace_ = dp(word1, word2, n1-1, n2-1);
            table[n1][n2] = min(min(delete_, insert_), replace_) + 1;
        }
        return table[n1][n2];
    }
};

在家做题，效率超低啊！可恶的病毒！